Question

【题目】如图，抛物线y=ax2+bx﹣4与x轴交于A（4，0）、B（﹣2，0）两点，与y轴交于点C，点P是线段AB上一动点（端点除外），过点P作PD∥AC，交BC于点D，连接CP．

（1）求该抛物线的解析式；

（2）当动点P运动到何处时，BP2=BDBC；

（3）当△PCD的面积最大时，求点P的坐标．

Answer 1

【答案】（1）；（2）（，0）；（3）（1，0）

【解析】

试题分析：（1）由抛物线y=ax2+bx﹣4过点A（4，0）、B（﹣2，0）根据待定系数法求解即可；

（2）设点P运动到点（x，0）时，有BP2=BDBC，在中，令x=0时，则y=﹣4，即可求得点C的坐标，由PD∥AC可得△BPD∽△BAC，再根据相似三角形的性质求解即可；

（3）由△BPD∽△BAC，根据相似三角形的性质及二次函数的性质求解即可.

（1）∵抛物线y=ax2+bx﹣4与x轴交于A（4，0）、B（﹣2，0）两点

∴，解得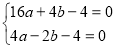

∴抛物线的解析式为；

（2）设点P运动到点（x，0）时，有BP2=BDBC，

在中，令x=0时，则y=﹣4

∴点C的坐标为（0，﹣4）

∵PD∥AC

∴△BPD∽△BAC

∴

∵，AB=6，BP=x﹣（﹣2）=x+2

∴，即

∵BP2=BDBC，

∴，解得x1=，x2=﹣2（不合题意，舍去）

∴点P的坐标是（，0）

∴当点P运动到（，0）时，BP2=BDBC；

（3）∵△BPD∽△BAC，

∴

∴，

又∵，

∴

∵＜0，∴当x=1时，S△BPC有最大值为3

∴点P的坐标为（1，0）时，△PDC的面积最大。