
【题目】如图1.直线AD∥EF,点B,C分别在EF和AD上,∠A=∠ABC,BD平分∠CBF.
(1)求证:AB⊥BD;
(2)如图2,BG⊥AD于点G,求证:∠ACB=2∠ABG;
(3)在(2)的条件下,如图3,CH平分∠ACB交BG于点H,设∠ABG=α,请直接写出∠BHC的度数.(用含α的式子表示)

【答案】(1)见解析;(2)见解析;(3)∠BHC=90°+∠α.
【解析】
(1)根据平行线的性质以及角平分线的定义,即可得到AB⊥BD;
(2)根据BG⊥AD,AD∥EF,可得∠FBG=∠AGB=90°,进而可得∠ABG=∠DBF,根据EF∥AD,即可得到∠ACB=∠CBF=2∠DBF=2∠ABG;
(3)根据平行线的性质以及角平分线的定义可得∠ABG=∠D=∠α,再根据∠HGC=90°即可得到∠BHC=∠HGC+∠ACH=90°+∠α.
解:(1)∵AD∥EF,
∴∠ABE=∠A=∠ABC,
又∵BD平分∠CBF,
∴∠CBD=∠FBD,
∴∠ABD=![]() (∠CBE+∠CBF)=
(∠CBE+∠CBF)=![]() ×180°=90°,
×180°=90°,
∴AB⊥BD;
(2)∵BG⊥AG,
∴∠FBG=∠AGB=90°,
∵∠ABD=90°,
∴∠ABG=∠DBF,
∵EF∥AD,
∴∠ACB=∠CBF=2∠DBF=2∠ABG;
(3)∵ AD∥EF,
∴∠D=∠DBF,
∴∠ACB=2∠DBF=2∠D,
∴∠D=![]() ∠ACB,
∠ACB,
∵CH平分∠ACB,
∴∠ACH=![]() ∠ACB,
∠ACB,
∴∠ACH=∠D,
∵∠ABG=∠D=α,
∴∠ACH=α,
∵BG⊥GC,
∴∠HGC=90°,
∴∠BHC=∠HGC+∠ACH=90°+∠α.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)探究发现
数学活动课上,小明说“若直线![]() 向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
经过一番讨论,小组成员展示了他们的解答过程:
在直线![]() 上任取点
上任取点![]() ,
,
向左平移3个单位得到点![]()
设向左平移3个单位后所得直线所对应的函数表达式为![]() .
.
因为![]() 过点
过点![]() ,
,
所以![]() ,
,
所以![]() ,
,
填空:所以平移后所得直线所对应函数表达式为
(2)类比运用
已知直线![]() ,求它关于
,求它关于![]() 轴对称的直线所对应的函数表达式;
轴对称的直线所对应的函数表达式;
(3)拓展运用
将直线![]() 绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人玩摸球游戏:一个不透明的袋子中装有相同大小的3个球,球上分别标有数字1,2,3.首先,甲从中随机摸出一个球,然后,乙从剩下的球中随机摸出一个球,比较球上的数字,较大的获胜.
(1)求甲摸到标有数字3的球的概率;
(2)这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠海市水务局对某小区居民生活用水情况进行了调査.随机抽取部分家庭进行统计,绘制成如下尚未完成的频数分布表和频率分布直方图.请根据图表,解答下列问题:
月均用水量(单位:吨 | 频数 | 频率 |
2≤x<3 | 4 | 0.08 |
3≤x<4 | a | b |
4≤x<5 | 14 | 0.28 |
5≤x<6 | 9 | c |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 5 | 0.1 |
合计 | d | 1.00 |

(1)b= ,c= ,并补全频数分布直方图;
(2)为鼓励节约用水用水,现要确定一个用水量标准P(单位:吨),超过这个标准的部分按1.5倍的价格收费,若要使60%的家庭水费支出不受影响,则这个用水量标准P= 吨;
(3)根据该样本,请估计该小区400户家庭中月均用水量不少于5吨的家庭约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.

(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上(点
上(点![]() 与点
与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,
,![]() 与边
与边![]() 相交于点
相交于点![]() ,与边
,与边![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)![]() 与
与![]() 有什么样的数量关系?请直接写出你的结论:____________________
有什么样的数量关系?请直接写出你的结论:____________________
(2)![]() 、
、![]() 、
、![]() 的数量之间具有怎样的关系?并证明你所得到的结论.
的数量之间具有怎样的关系?并证明你所得到的结论.
(3)如果正方形的边长是1,![]() ,直接写出点
,直接写出点![]() 到直线
到直线![]() 的距离.
的距离.

解:(1)![]() 与
与![]() 的数量关系:____________________
的数量关系:____________________
(2)![]() 、
、![]() 、
、![]() 的数量之间的关系是 .
的数量之间的关系是 .
证明:
(3)点![]() 到直线
到直线![]() 的距离是 .
的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
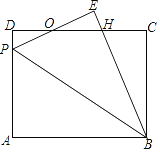
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH.
(2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程.
试题解析:
(1)解:证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH,
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH.
(2)解:设DP=x,则EH=x,BH=10﹣x,
CH=CD﹣DH=CD﹣PE=10﹣(8﹣x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10﹣x)2,
∴x=![]() ,
,
∴DP=![]() .
.
【题型】解答题
【结束】
25
【题目】某文教店老板到批发市场选购A,B两种品牌的绘图工具套装,每套A品牌套装进价比B品牌每套套装进价多2.5元,已知用200元购进A种套装的数量是用75元购进B种套装数量的2倍.
(1)求A,B两种品牌套装每套进价分别为多少元?
(2)若A品牌套装每套售价为13元,B品牌套装每套售价为9.5元,店老板决定,购进B品牌的数量比购进A品牌的数量的2倍还多4套,两种工具套装全部售出后,要使总的获利超过120元,则最少购进A品牌工具套装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊的毕达哥拉斯学派由古希腊哲学家毕达哥拉斯所创立,毕达哥拉斯学派认为数是万物的本原,事物的性质是由某种数量关系决定的,如他们研究各种多边形数:记第n个k边形数N(n,k)=![]() n2+
n2+![]() n(n≥1,k≥3,k、n都为整数),
n(n≥1,k≥3,k、n都为整数),
如第1个三角形数N(1,3)=![]() ×12+
×12+![]() ×1=1;
×1=1;
第2个三角形数N(2,3)=![]() ×22+
×22+![]() ×2=3;
×2=3;
第3个四边形数N(3,4)=![]() ×32+
×32+![]() ×3=9;
×3=9;
第4个四边形数N(4,4)=![]() ×42+
×42+![]() ×4=16.
×4=16.
(1)N(5,3)=________,N(6,5)=________;
(2)若N(m,6)比N(m+2,4)大10,求m的值;
(3)若记y=N(6,t)-N(t,5),试求出y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com