练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在方格纸中，假设每个小正方形的面积为2，则图中的四条线段中长度是有理数的有多少条。
    [     ]

    A.1
    B.2
    C.3
    D.4

    B
    练习册系列答案
  • 出彩同步大试卷系列答案
  • 黄冈状元成才路状元导学案系列答案
  • 全优天天练系列答案
  • 学习高手课时作业系列答案
  • 鲁西图书课时训练系列答案
  • 优学3部曲初中生随堂检测系列答案
  • 非常听力系列答案
  • 优效作业本系列答案
  • 天利38套对接高考小题轻松练系列答案
  • 抢先起跑提优大试卷系列答案
    • 年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图1，AD和AE分别是△ABC的BC边上的高和中线，点D是垂足，点E是BC的中点，规定：λA=
    DEBE
    ．特别地，当点D、E重合时，规定：λA=0．另外，对λB、λC作类似的规定．
    精英家教网
    （1）如图2，在△ABC中，∠C=90°，∠A=30°，求λA、λC；
    （2）在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且λA=2，面积也为2；
    （3）判断下列三个命题的真假（真命题打“√”，假命题打“×”）：
    ①若△ABC中λA＜1，则△ABC为锐角三角形；
     

    ②若△ABC中λA=1，则△ABC为直角三角形；
     

    ③若△ABC中λA＞1，则△ABC为钝角三角形．
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    操作探究：
    我们知道一个三角形中有三条高线和三条中线．如图1，AD和AE分别是△ABC中BC边上的高线和中线，我们规定：kA=
    DE
    BE′
    ，另外，对kB、kC作类似的规定．
    （1）如图2，在△ABC中，∠C=90°，∠A=30°，则kA的值为
    1
    1
    ，kC的值为
    1
    2
    1
    2
    ；
    （2）在每个小正方形边长均为1的4×4的方格纸上（如图3），画一个△ABC，使其顶点在格点（格点即每个小正方形的顶点）上，且kA=2，面积也为2；
    （3）判断下面三个命题的真假（真命题打“√”，假命题的打“×”）
    ①若△ABC中，kA＜1，则△ABC为锐角三角形
    ×
    ×
    ；
    ②若△ABC中，kA=1，则△ABC为直角三角形
    √
    √
    ；
    ③若△ABC中，kA＞1，则△ABC为钝角三角形
    √
    √
    ．

    查看答案和解析>>

    科目：初中数学 来源：浙江省台州市2011年中考数学试题 题型：059

    如图，AD和AE分别是△ABC的BC边上的高和中线，点D是垂足，点E是BC的中点，规定：λA＝．特别地，当点D、E重合时，规定：λA＝0．另外，对λB、λC作类似的规定．

    (1)如图，在△ABC中，∠C＝90o，∠A＝30o，求λA、λC；

    (2)在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点(格点即每个小正方形的顶点)上，且λA＝2，面积也为2；

    (3)判断下列三个命题的真假(真命题打“√”，假命题打“×”)：

    ①若△ABC中λA＜1，则△ABC为锐角三角形；(　　)

    ②若△ABC中λA＝1，则△ABC为锐角三角形；(　　)

    ③若△ABC中λA＞1，则△ABC为锐角三角形．(　　)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

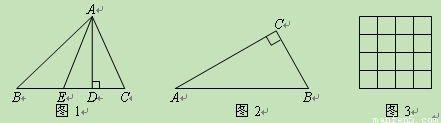
    （11·台州）(12分)如图1，AD和AE分别是△ABC的BC边上的高和中线，

    点D是垂足，点E是BC的中点，规定：．特别地，当点D、E重合时，规定：λA

    ＝0．另外，对λB、λC作类似的规定．

    (1)如图2，在△ABC中，∠C＝90º，∠A＝30º，求λA、λC；

    (2)在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点(格点即每个小正方形的顶点)上，且λA＝2，面积也为2；

    (3)判断下列三个命题的真假(真命题打“P”，假命题打“×”)：

    ①若△ABC中λA＜1，则△ABC为锐角三角形；【    】

    ②若△ABC中λA＝1，则△ABC为锐角三角形；【    】

    ③若△ABC中λA＞1，则△ABC为锐角三角形．【    】

     

    查看答案和解析>>

    科目：初中数学 来源：2011年初中毕业升学考试（湖南郴州卷）数学 题型：解答题

    （11·台州）(12分)如图1，AD和AE分别是△ABC的BC边上的高和中线，

    点D是垂足，点E是BC的中点，规定：．特别地，当点D、E重合时，规定：λA

    ＝0．另外，对λB、λC作类似的规定．

    (1)如图2，在△ABC中，∠C＝90º，∠A＝30º，求λA、λC；

    (2)在每个小正方形边长均为1的4×4的方格纸上，画一个△ABC，使其顶点在格点(格点即每个小正方形的顶点)上，且λA＝2，面积也为2；

    (3)判断下列三个命题的真假(真命题打“P”，假命题打“×”)：

    ①若△ABC中λA＜1，则△ABC为锐角三角形；【    】

    ②若△ABC中λA＝1，则△ABC为锐角三角形；【    】

    ③若△ABC中λA＞1，则△ABC为锐角三角形．【    】

     

    查看答案和解析>>

    同步练习册答案