
分析 (1)将原式展开化简可得4(3n-5),根据n是自然数可知原式能被4整除;
(2)先根据误乘的结果用除法求出原多项式,再用该多项式除以$\frac{1}{2}$a可得结果.
解答 解:(1)能,
原式=n2+3n-(n2-5n-4n+20)
=n2+3n-n2+5n+4n-20
=12n-20
=4(3n-5),
因为n是自然数,所以3n-5是整数,
因此原式能被4整除;
(2)根据题意,原多项式为(8a4b-4a3+2a2)÷$\frac{1}{2}$a=16a3b-8a2+4a.
故正确结果为:(16a3b-8a2+4a)÷$\frac{1}{2}$a=32a2b-16a+8.
点评 本题主要考查整式的运算能力,熟练掌握多项式与单项式相乘、除,多项式与多项式相乘的运算法则是关键也是基础.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
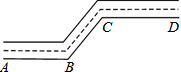 如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=150°,当街道AB和CD平行时,∠BCD=150度,根据是两直线平行,内错角相等.
如图所示,一条街道的两个拐角∠ABC和∠BCD,若∠ABC=150°,当街道AB和CD平行时,∠BCD=150度,根据是两直线平行,内错角相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
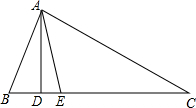 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com