
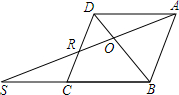
 菱形ABCD中,O对角线BD上一点,连接AO并延长,与DC交于点R,与BC的延长线交于点S,若AD=4,∠DCB=60°,BS=10,求CR、OD和AR的长.
菱形ABCD中,O对角线BD上一点,连接AO并延长,与DC交于点R,与BC的延长线交于点S,若AD=4,∠DCB=60°,BS=10,求CR、OD和AR的长. 分析 由菱形的性质得DC=CB=DA=4,AD∥BC,再由∠DCB=60°得到△BCD为等边三角形,则BD=BC=4,作AH⊥BC于H,如图,在Rt△ABH中计算出BH=$\frac{1}{2}$AB=2,AH=$\sqrt{3}$BH=2$\sqrt{3}$,在Rt△AHS中利用勾股定理计算出AS=2$\sqrt{39}$,接着证明△ADO∽△SBO,利用相似比得到DO:BO=4:10=2:5,则DO=$\frac{2}{7}$BD=$\frac{8}{7}$;然后证明△ADR∽△SCR,利用相似比得到DR:CR=AR:SR=2:3,于是得到CR=$\frac{3}{5}$CD=$\frac{12}{5}$,AR=$\frac{2}{5}$AS=$\frac{4\sqrt{39}}{5}$.
解答 解:∵菱形ABCD中,AD=4,
∴DC=CB=DA=4,AD∥BC,
∵∠DCB=60°,
∴△BCD为等边三角形,
∴BD=BC=4,
作AH⊥BC于H,如图,
在Rt△ABH中,∵∠ABH=∠DCB=60°
∴BH=$\frac{1}{2}$AB=2,AH=$\sqrt{3}$BH=2$\sqrt{3}$,
在Rt△AHS中,AS=$\sqrt{A{H}^{2}+S{H}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+1{2}^{2}}$=2$\sqrt{39}$,
∵AD∥BS,
∴△ADO∽△SBO,
∴AD:BS=DO:BO,即DO:BO=4:10=2:5,
∴DO=$\frac{2}{7}$BD=$\frac{8}{7}$;
∵AD∥SC,
∴△ADR∽△SCR,
∴AD:CR=DR:CR=AR:SR,即DR:CR=AR:SR=4:(10-4)=2:3,
∴CR=$\frac{3}{5}$CD=$\frac{12}{5}$,AR=$\frac{2}{5}$AS=$\frac{4\sqrt{39}}{5}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;利用相似三角形的性质主要是利用相似比计算相应线段的长.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
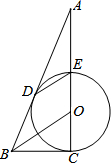 如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.
如图,CE是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线,交CE延长线于点A,连接DE,过点O作OB∥ED,交AD的延长线于点B,连接BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.
甲、乙两个工程队共同修建一条乡镇公路,甲队按一定的工作效率先施工,一段时间后,乙队从另一端按一定的工作效率加入施工,中途乙队遇到山坡路段,工作效率降低,当乙队完成山坡路段时恰好公路修建完成,此时甲队工作了60天,设甲、乙两队各自修建的公路的长度为y(米),甲队工作时间为x(天),y与x之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
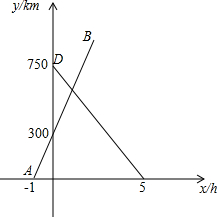 铁路中心记录途经南京的各型号列车行驶情况,如图,上午7:00为起始时间,列车x小时后距南京y千米,线段AB和DE分别表示一辆动车和一辆特快列车行驶过程中y与x的函数关系,点A坐标为(-1,0),点B坐标为(2,900).
铁路中心记录途经南京的各型号列车行驶情况,如图,上午7:00为起始时间,列车x小时后距南京y千米,线段AB和DE分别表示一辆动车和一辆特快列车行驶过程中y与x的函数关系,点A坐标为(-1,0),点B坐标为(2,900).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
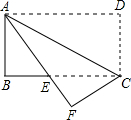 如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.
如图,在长方形纸片ABCD中,AB=8,AD=16,将它沿着对角线AC对折,使点D落在点F处,AF交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1与(-4)+(-3) | B. | 3与-(-3) | C. | $\frac{3^2}{4}$与$\frac{9}{16}$ | D. | |-16|与-16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com