
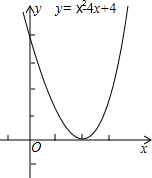
 (1)抛物线与x轴有1个交点,它们的横坐标是2;
(1)抛物线与x轴有1个交点,它们的横坐标是2; 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1,$\sqrt{2}$,3 | B. | $\sqrt{2}$,$\sqrt{3}$,5 | C. | 1.5,2,2.5 | D. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
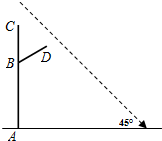 如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?
如图,铜亭广场装有智能路灯,路灯设备由灯柱AC与支架BD共同组成(点C处装有安全监控,点D处装有照明灯),灯柱AC为6米,支架BD为2米,支点B到A的距离为4米,AC与地面垂直,∠CBD=60°.某一时刻,太阳光与地面的夹角为45°,求此刻路灯设备在地面上的影长为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
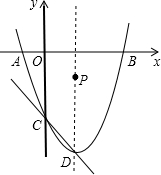 如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为D,问:在抛物线的对称轴上是否存在一点P,使得以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,求出点P 的坐标;若不存在,说明理由.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为D,问:在抛物线的对称轴上是否存在一点P,使得以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,求出点P 的坐标;若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com