
【题目】甲地捐赠了600吨物资支援武汉抗击新冠肺炎,准备安排A、B两种类型的货车把这批物资从甲地快速送到武汉,若安排A型货车5辆、B型货车6辆,一共需补贴油费3800元;若安排A型货车3辆、B型货车2辆,一共需补贴油费1800元.
(1)从甲地到武汉,A、B两种类型货车每辆各需补贴油费多少元?
(2)A型货车每辆可装15吨物资,B型货车每辆可装12吨物资,若安排的B型货车的数量是A型货车的2倍还多4辆,且A型车最多可安排18辆.运送这批物资共有哪些安排,其中补贴的总油费最少是多少元?
【答案】(1)从甲地到武汉,每辆![]() 型货车补贴油费400元,每辆
型货车补贴油费400元,每辆![]() 型货车补贴油费300元;(2)运送这批物资,不同安排中,补贴的总的油费最少是16200元.
型货车补贴油费300元;(2)运送这批物资,不同安排中,补贴的总的油费最少是16200元.
【解析】
(1)设从甲地到武汉,每辆A型货车补贴油费x元,每辆B型货车补贴油费y元,根据“从甲地到武汉,A型货车5辆、B型货车6辆,一共需补贴油费3800元;A型货车3辆、B型货车2辆,一共需补贴油费1800元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设安排A型货车m辆,则安排B型货车(2m+4)辆,根据A型车最多可安排18辆且安排的车辆总的装载量不低于600吨,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为整数即可得出m的值,再求出各安排方案所需补贴的总的油费,比较后即可得出结论.
(1)设从甲地到武汉,每辆![]() 型货车补贴油费
型货车补贴油费![]() 元,每辆
元,每辆![]() 型货车补贴油费
型货车补贴油费![]() 元,
元,
依题意,得:![]() ,解得
,解得![]() .
.
答:从甲地到武汉,每辆![]() 型货车补贴油费400元,每辆
型货车补贴油费400元,每辆![]() 型货车补贴油费300元.
型货车补贴油费300元.
(2)设安排![]() 型货车
型货车![]() 辆,则安排
辆,则安排![]() 型货车
型货车![]() 辆,
辆,
依题意得![]() .解得
.解得![]() .
.
![]() 为正整数,
为正整数,![]() ,16,17,18
,16,17,18
当![]() 时,补贴的总的油费为
时,补贴的总的油费为![]() (元
(元![]() ;
;
当![]() 时,补贴的总的油费为
时,补贴的总的油费为![]() (元
(元![]() ;
;
当![]() 时,补贴的总的油费为
时,补贴的总的油费为![]() (元
(元![]() ;
;
当![]() 时,补贴的总的油费为
时,补贴的总的油费为![]() (元
(元![]() .
.
![]() ,
,
![]() 运送这批物资,不同安排中,补贴的总的油费最少是16200元.
运送这批物资,不同安排中,补贴的总的油费最少是16200元.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小明在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线相互垂直的三角形“中垂三角形”,如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
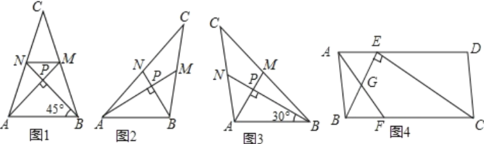
(特例研究)
(1)如图1,当tan∠PAB=1,c=4![]() 时,a=b= ;
时,a=b= ;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图2证明你的结论;
(拓展证明)
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF交BE相较于点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD的顶点A在反比例函数y=![]() (x>0)的图象上,函数y=
(x>0)的图象上,函数y=![]() (k>5,x>0)的图象关于直线AC对称,且经过点B、D两点.若AB=2,∠DAB=30°,如下结论:①O、A、C三点在同一直线上;②点A的横坐标是
(k>5,x>0)的图象关于直线AC对称,且经过点B、D两点.若AB=2,∠DAB=30°,如下结论:①O、A、C三点在同一直线上;②点A的横坐标是![]() ;③点D的坐标是(
;③点D的坐标是(![]() +1,2
+1,2![]() );④比例系数k的值为10+
);④比例系数k的值为10+![]() .其中不正确的结论是( )
.其中不正确的结论是( )
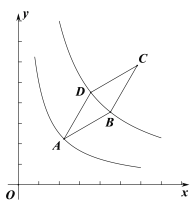
A.①②③B.②③④C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )

A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=5cm,BD=8cm.点P从点B出发,沿BA方向匀速运动,速度为![]() ;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点P作PN∥BC分别交BD,CD于点M,N,连接QM,QN.设运动时间为
;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点P作PN∥BC分别交BD,CD于点M,N,连接QM,QN.设运动时间为![]() .解答下列问题:
.解答下列问题:
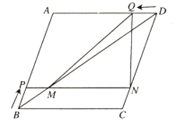
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() 的面积为菱形
的面积为菱形![]() 面积的
面积的![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)是否存在某一时刻![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出
为等腰三角形?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 的边
的边![]() 上存在点
上存在点![]() ,使得
,使得![]() ,我们称点
,我们称点![]() 为矩形的“和谐点
为矩形的“和谐点
(1)求证: ![]() ;
;
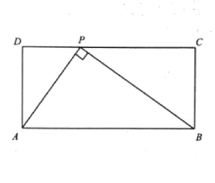
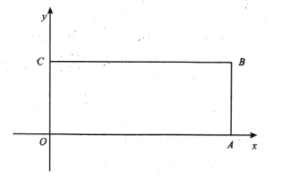
(2)如图2,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() 为坐标原点,点
为坐标原点,点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,在
轴上,在![]() 边上是否存在“和谐点”
边上是否存在“和谐点”![]() ,如果存在,求出点
,如果存在,求出点![]() 的坐标;如果不存在,请说明理由
的坐标;如果不存在,请说明理由
(3)在(2)中,如果点![]() 的坐标为
的坐标为![]() ,且在
,且在![]() 上存在“和谐点”
上存在“和谐点”![]() 求
求![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com