
【题目】如图所示,菱形ABCD的顶点A在反比例函数y=![]() (x>0)的图象上,函数y=
(x>0)的图象上,函数y=![]() (k>5,x>0)的图象关于直线AC对称,且经过点B、D两点.若AB=2,∠DAB=30°,如下结论:①O、A、C三点在同一直线上;②点A的横坐标是
(k>5,x>0)的图象关于直线AC对称,且经过点B、D两点.若AB=2,∠DAB=30°,如下结论:①O、A、C三点在同一直线上;②点A的横坐标是![]() ;③点D的坐标是(
;③点D的坐标是(![]() +1,2
+1,2![]() );④比例系数k的值为10+
);④比例系数k的值为10+![]() .其中不正确的结论是( )
.其中不正确的结论是( )
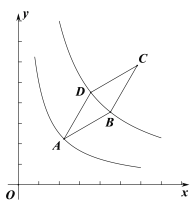
A.①②③B.②③④C.①③④D.①②④
【答案】B
【解析】
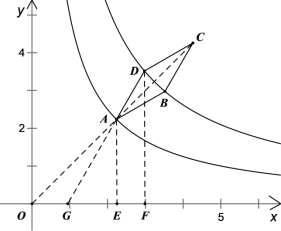
如图(见解析),连接OC、AC,过点A作![]() 轴于点E,过点D作
轴于点E,过点D作![]() 轴于点F,延长DA,与x轴交于点G,先根据轴对称的性质得出O、A、C三点在同一直线上,且
轴于点F,延长DA,与x轴交于点G,先根据轴对称的性质得出O、A、C三点在同一直线上,且![]() ,再利用反比例函数的性质、等腰三角形的性质求出点A的坐标,进而可求出点D的坐标,然后利用待定系数法可求出k的值.
,再利用反比例函数的性质、等腰三角形的性质求出点A的坐标,进而可求出点D的坐标,然后利用待定系数法可求出k的值.
如图,连接OC、AC,过点A作![]() 轴于点E,过点D作
轴于点E,过点D作![]() 轴于点F,延长DA,与x轴交于点G,则
轴于点F,延长DA,与x轴交于点G,则![]()
![]() 函数
函数![]() 的图象关于直线AC对称
的图象关于直线AC对称
![]() O、A、C三点在同一直线上,且
O、A、C三点在同一直线上,且![]() ,则结论①正确
,则结论①正确
![]()
设![]() ,则点
,则点![]()
将![]() 代入函数
代入函数![]() 得:
得:![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]()
即点A的横坐标为![]() ,则结论②不正确
,则结论②不正确
![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
![]() ,
,![]()
![]()
![]()
则在![]() 中,
中,![]() ,
,![]()
![]()
![]()
![]() 点D的坐标为
点D的坐标为![]() ,则结论③不正确
,则结论③不正确
![]() 点
点![]() 在函数
在函数![]() 的图象上
的图象上
则![]()
解得![]() ,则结论④不正确
,则结论④不正确
综上,不正确的结论是②③④
故选:B.


科目:初中数学 来源: 题型:
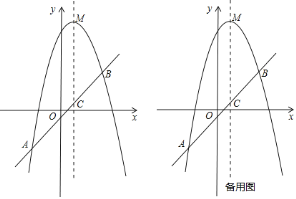
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,
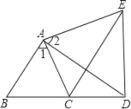
(1)试说明△ABD与△ACE全等的理由;
(2)如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有三条边相等的四边形称为三等边四边形.
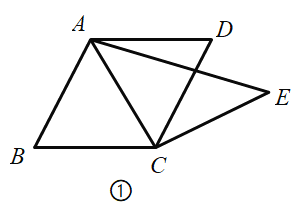
(1)如图①,平行四边形![]() 中,对角线
中,对角线![]() 平分
平分![]() ,将线段
,将线段![]() 绕点
绕点![]() 旋转一个角度
旋转一个角度![]() 至
至![]() ,连接
,连接![]() .
.
①求证:四边形![]() 是三等边四边形;
是三等边四边形;
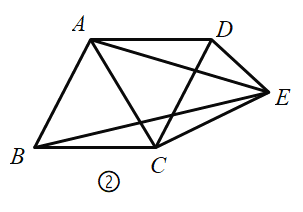
②如图②,连接![]() ,
,![]() .求证:
.求证:![]() ;
;
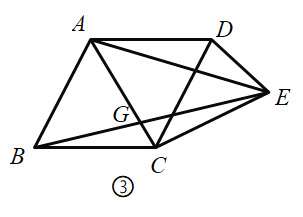
(2)如图,在(1)的条件下,设![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,
,![]() ,求以
,求以![]() ,
,![]() 和
和![]() 为边的三角形的面积.
为边的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲地捐赠了600吨物资支援武汉抗击新冠肺炎,准备安排A、B两种类型的货车把这批物资从甲地快速送到武汉,若安排A型货车5辆、B型货车6辆,一共需补贴油费3800元;若安排A型货车3辆、B型货车2辆,一共需补贴油费1800元.
(1)从甲地到武汉,A、B两种类型货车每辆各需补贴油费多少元?
(2)A型货车每辆可装15吨物资,B型货车每辆可装12吨物资,若安排的B型货车的数量是A型货车的2倍还多4辆,且A型车最多可安排18辆.运送这批物资共有哪些安排,其中补贴的总油费最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
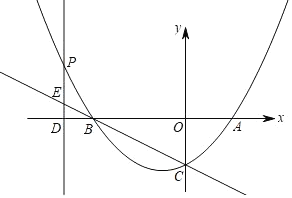
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛.为了了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调査结果绘制成的统计图(部分)如图

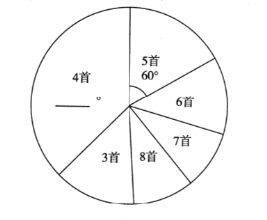
大赛结束后一个月,再次抽查这部分学生的周诗词诵背数量,绘制成如下统计表:
诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息分析
(1)学校团委一共抽取了多少名学生进行调查
(2)大赛前诵背4首人数所在扇形的圆心角为 ,并补充完条形统计图
(3)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com