
【题目】如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,
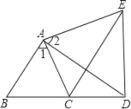
(1)试说明△ABD与△ACE全等的理由;
(2)如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
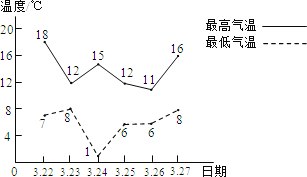
【题目】如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况.
(1)最低气温的中位数是 ℃;3月24日的温差是 ℃;
(2)分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;
(3)经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?
查看答案和解析>>
科目:初中数学 来源: 题型:
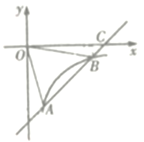
【题目】如图,已知一次函数y= kx +b的图象交反比例函数![]() 的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
(1)求这两个函数的解析式;
(2)连接QA、OB.求△AOB的面积;
(3)请直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
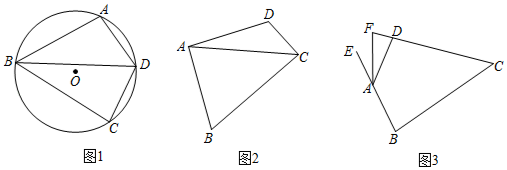
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
![]() 如图1,点
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
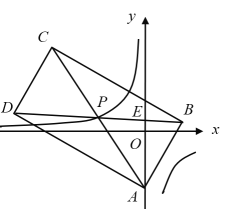
(1)求![]() 的值;
的值;
(2)若将矩形![]() 向下平移
向下平移![]() 个单位,使点
个单位,使点![]() 落在反比例函数
落在反比例函数![]() 的图象上,求
的图象上,求![]() 的值;
的值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小明在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线相互垂直的三角形“中垂三角形”,如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
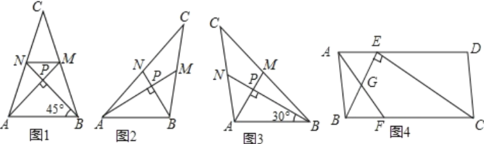
(特例研究)
(1)如图1,当tan∠PAB=1,c=4![]() 时,a=b= ;
时,a=b= ;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图2证明你的结论;
(拓展证明)
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF交BE相较于点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
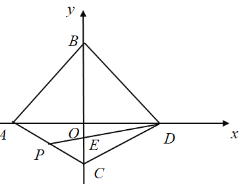
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,直线
为坐标原点,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 在
在![]() 轴负半轴上,且
轴负半轴上,且![]() ,把
,把![]() 沿
沿![]() 轴翻折,使点
轴翻折,使点![]() 落在
落在![]() 轴上的点
轴上的点![]() 处,点
处,点![]() 为线段
为线段![]() 上一点,连接
上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,则直线
,则直线![]() 的解析式为__________.
的解析式为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
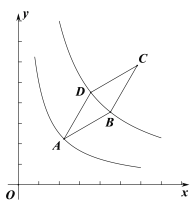
【题目】如图所示,菱形ABCD的顶点A在反比例函数y=![]() (x>0)的图象上,函数y=
(x>0)的图象上,函数y=![]() (k>5,x>0)的图象关于直线AC对称,且经过点B、D两点.若AB=2,∠DAB=30°,如下结论:①O、A、C三点在同一直线上;②点A的横坐标是
(k>5,x>0)的图象关于直线AC对称,且经过点B、D两点.若AB=2,∠DAB=30°,如下结论:①O、A、C三点在同一直线上;②点A的横坐标是![]() ;③点D的坐标是(
;③点D的坐标是(![]() +1,2
+1,2![]() );④比例系数k的值为10+
);④比例系数k的值为10+![]() .其中不正确的结论是( )
.其中不正确的结论是( )
A.①②③B.②③④C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
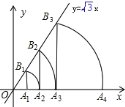
【题目】如图,直线![]() ,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2020的坐标为______________.
,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A2020的坐标为______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com