
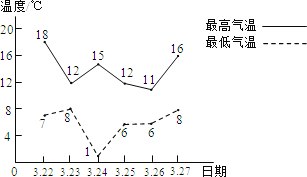
【题目】如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况.
(1)最低气温的中位数是 ℃;3月24日的温差是 ℃;
(2)分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;
(3)经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?
【答案】(1)6.5;14; (2)3月22日至27日间的最高气温的平均数是14℃,最低气温的平均数是6℃;(3)数据更稳定的是最低气温.
【解析】
(1)将最低气温按照从低到高进行排列,按照中位数的计算方法进行计算;温差用最高气温减去最低气温即可;
(2)按照平均数的计算方法计算即可;
(3)方差小则稳定,方差大则不稳定,进行判断即可.
解:(1)由图知,最低气温从低到高排列为:1,6,6,7,8,8
所以最低气温的中位数为:![]()
由图知:3.24日的最高气温为:15℃,最低气温为1℃,
所以3.24日的气温差为:15℃-1℃=14℃
(2)最高气温平均数:![]() ×(18+12+15+12+11+16)=14(℃);
×(18+12+15+12+11+16)=14(℃);
最低气温平均数:![]() ×(7+8+1+6+6+8)=6(℃);
×(7+8+1+6+6+8)=6(℃);
即3月22日至27日间的最高气温的平均数是14℃,最低气温的平均数是6℃;
(3)因为最高气温的方差为6.33,,最低气温的方差为5.67
所以6.33![]() 5.67
5.67
故数据更稳定的是最低气温.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
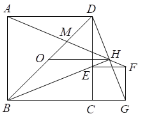
【题目】如图,四边形ABCD、CEFG都是正方形,E在CD上且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,下列四个结论:
① BE⊥GD; ② OH=![]() BG; ③ ∠AHD=45°; ④ GD=
BG; ③ ∠AHD=45°; ④ GD=![]() AM.
AM.
其中正确的结论个数有
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为![]() ,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是____________
,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是____________

①∠DAE=∠DEA;②∠DMC=45°;③![]() ;④若MH=2,则S△CMD=
;④若MH=2,则S△CMD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() .
.
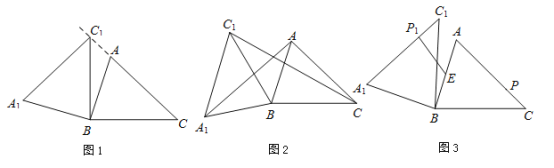
(1)如图1,当点![]() 在线段
在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
(2)如图2,连接![]() ,
,![]() .若
.若![]() 的面积为4,求
的面积为4,求![]() 的面积;
的面积;
(3)如图3,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转过程中,点
按逆时针方向旋转过程中,点![]() 的对应点是点
的对应点是点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饰品店老板去批发市场购买新款手链,第一次购手链共用1000元,将该手链以每条定价28元销售,并很快售完,所得利润率高于30%.由于该手链深得年轻人喜爱,十分畅销,第二次去购进手链时,每条的批发价已比第一次高5元,共用去了1500元,所购数量比第一次多10条.当这批手链以每条定价32元售出80%时,出现滞销,便以5折价格售完剩余的手链.现假设第一次购进手链的批发价为x元/条.
(1)用含x的代数式表示:第一次购进手链的数量为 条;
(2)求x的值;
(3)不考虑其他因素情况下,试问该老板第二次售手链是赔钱了,还是赚钱了?若赔钱,赔多少?若赚钱,赚多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
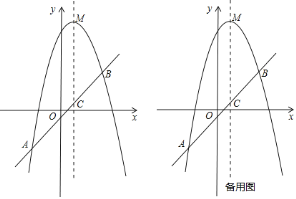
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,
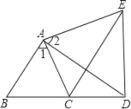
(1)试说明△ABD与△ACE全等的理由;
(2)如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com