
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .


【答案】(1)全等,理由见解析;(2)120°;(3)![]() .
.
【解析】
(1)结论:△ABD≌△ACE.根据SAS证明即可.
(2)利用全等三角形的性质解决问题即可.
(3)如图b中,AD交AE于J.设△ABC的外接圆的圆心为K.证明∠AOC=120°,推出点O的运动轨迹是K为圆心,KC半径的圆弧,圆心角为60°从而可以求得运动的轨迹.
解:(1)结论:△ABD≌△ACE.
∵△ADE是由△ABC绕点A旋转θ得到,∴△ABC是等边三角形.
∴AB=AD=AC=AE,∠BAD=∠CAE=20°,
在△ABD与△ACE中,∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).
(2)由已知得:△ABC和△ADE是全等的等边三角形,∴AB=AD=AC=AE.
∵△ADE是由△ABC绕点A旋转θ得到的,∴∠BAD=∠CAE=θ.
∴△BAD≌△CAE(SAS).∴∠ADB=∠AEC.
∵∠ADB+∠ABD+∠BAD=180°,∴∠AEC+∠ABO+∠BAD=180°.
∵∠ABO+∠AEC+∠BAE+∠BOE=360°,∠BAE=∠BAD+∠DAE,
∴∠DAE+∠BOE=180°.
又∵∠DAE=60°,∴∠BOE=120°.
(3)如图b中,AD交AE于J.设△ABC的外接圆的圆心为K.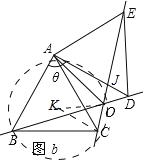
∵△ABD≌△ACE,
∴∠ODJ=∠AEJ,
∵∠AJE=∠OJD,
∴∠EAJ=∠JOD=60°,
∴∠AOC=120°,
∴点O的运动轨迹是K为圆心,KC半径的圆弧,圆心角为60°.
∴当θ从60°到120°的旋转过程中,运动的轨迹为![]() =
=![]() ,
,
故答案为:![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】数学课上,李老师准备了四张背面都一样的卡片A、B、C、D,每张卡片的正面标有字母a、b、c表示三条线段(如下图).把四张卡片背面朝上放在桌面上,李老师从这四张卡片中随机抽取一张卡片后不放回,再随机抽取一张.

⑴ 李老师随机抽取一张卡片,抽到卡片B的概率等于 ;
⑵ 求李老师抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,P为BA延长线上一点,点C在⊙O上,连接PC,D为半径OA上一点,PD=PC,连接CD并延长交⊙O于点E,且E是![]() 的中点.
的中点.
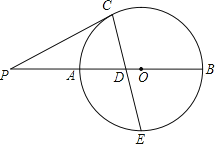
(1)求证:PC是⊙O的切线;
(2)若AB=8,CDDE=15,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,半圆O的直径AB=4,![]() =
=![]() ,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
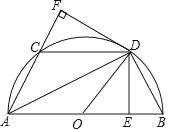
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
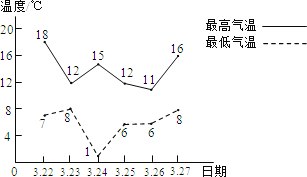
【题目】如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况.
(1)最低气温的中位数是 ℃;3月24日的温差是 ℃;
(2)分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;
(3)经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,管中放置着三根同样的绳子AA1、BB1、CC1;
(1)小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?
(2)小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校计划举行社会实践活动,现随机抽取了部分学生进行主题为“你最想去的地点是?”的问卷调查,要求学生必须从“A(大鹏所城),B(园山),C(西冲),D(欢乐谷)”四个景点中选择一项,根据调查结果,绘制了如图两幅不完整的统计图,请你根据图中所提供的信息,完成下列问题:
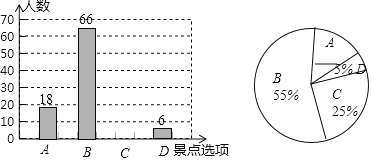
(1)本次调查的学生人数为 人;
(2)在扇形统计图中,“园山”部分所占圆心角的度数为 ;
(3)请将两幅统计图补充完整;
(4)若该校共有3000名学生,估计该校最想去大鹏所城的学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小明在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线相互垂直的三角形“中垂三角形”,如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
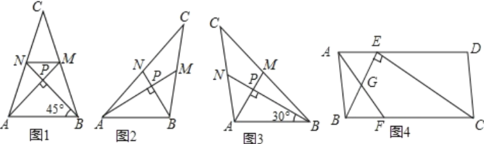
(特例研究)
(1)如图1,当tan∠PAB=1,c=4![]() 时,a=b= ;
时,a=b= ;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图2证明你的结论;
(拓展证明)
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF交BE相较于点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com