
【题目】如图,管中放置着三根同样的绳子AA1、BB1、CC1;
(1)小明从这三根绳子中随机选一根,恰好选中绳子AA1的概率是多少?
(2)小明先从左端A、B、C三个绳头中随机选两个打一个结,再从右端A1、B1、C1三个绳头中随机选两个打一个结,求这三根绳子能连结成一根长绳的概率.
![]()
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 交y轴于点A(0,4),交x轴于点B(4,0)、C,点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作
交y轴于点A(0,4),交x轴于点B(4,0)、C,点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作![]() 于点Q,连接AP(AP不平行x轴).
于点Q,连接AP(AP不平行x轴).
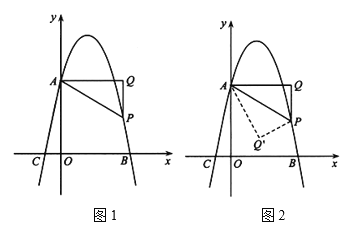
(1)求抛物线的解析式;
(2)点P在抛物线上运动,若![]() ∽
∽![]() (点P与点C对应),求点P的坐标;
(点P与点C对应),求点P的坐标;
(3)如图2,若点P位于抛物线的对称轴的右侧,将![]() 沿AP对折,点Q的对应点为点
沿AP对折,点Q的对应点为点![]() ,当点
,当点![]() 落在x轴上时,求点P的坐标.
落在x轴上时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
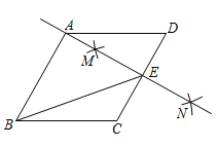
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
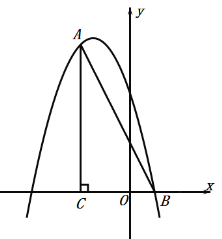
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.
①求点P的坐标和PE的最大值.
②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为2![]() ﹣6;④当OD⊥AD时,BP=2.其中结论正确的有( )
﹣6;④当OD⊥AD时,BP=2.其中结论正确的有( )
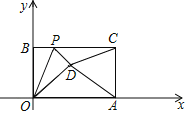
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )
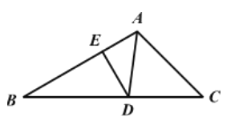
A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是被誉为“川北第一楼”的凤凰楼,它不仅是广元市的城标,更是一份承传文化的载体.李铭和王华同学想借助无人机测量凤凰楼的高度,如图②为测量示意图,他们站在坡度是![]() ,坡面长为
,坡面长为![]() 的斜坡
的斜坡![]() 的坡底
的坡底![]() 处操控无人机,无人机从坡顶
处操控无人机,无人机从坡顶![]() 出发,以
出发,以![]() 的速度,沿仰角
的速度,沿仰角![]() 的方向爬升,
的方向爬升,![]() 时到达空中的
时到达空中的![]() 处.
处.
(1)求此时无人机离坡底![]() 所在地面的高度;
所在地面的高度;
(2)如图②,无人机在![]() 处测得凤凰楼顶部
处测得凤凰楼顶部![]() 的仰角为
的仰角为![]() ,底部
,底部![]() 的俯角为
的俯角为![]() (凤凰楼与李铭和王华所站坡底
(凤凰楼与李铭和王华所站坡底![]() 在同一水平面),求凤凰楼的高度
在同一水平面),求凤凰楼的高度![]() .
.
(结果精确到![]() ;参考数据:
;参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
图① 图②
图②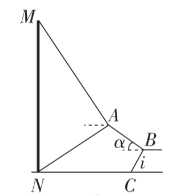
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小聪参加了![]() 跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如图的两个统计图.
跑的5期集训,每期集训结束时进行测试,根据他们的集训时间、测试成绩绘制成如图的两个统计图.
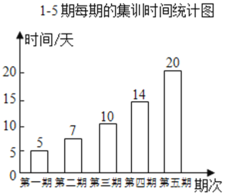
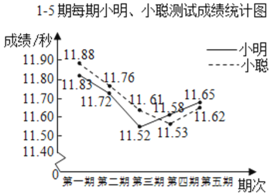
根据图中信息,有下面四个推断:
①这5期的集训共有56天;
②小明5次测试的平均成绩11.66秒;
③从集训时间看,集训时间不是越长越好,集训时间过长,可能造成劳累,导致成绩下滑;
④从测试成绩看,两人的最好成绩都是在第4期出现,建议集训时间定为14天.
你认为合理的推断是__________(填写你认为正确的推断序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com