
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁЯACB=90ЁуЃЌOC=2OBЃЌtanЁЯABC=2ЃЌЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎХзЮяЯпy=Љx2+bx+cОЙ§AЁЂBСНЕуЃЎ
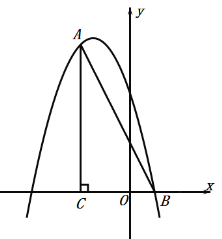
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧжБЯпABЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌЙ§ЕуPзїPDДЙжБxжсгкЕуDЃЌНЛЯпЖЮABгкЕуEЃЌЪЙPEзюДѓЃЎ
ЂйЧѓЕуPЕФзјБъКЭPEЕФзюДѓжЕЃЎ
ЂкдкжБЯпPDЩЯЪЧЗёДцдкЕуMЃЌЪЙЕуMдквдABЮЊжБОЖЕФдВЩЯЃЛШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2Љ3x+4ЃЛЃЈ2ЃЉЂй![]() ЃЌP
ЃЌP![]() Ђк MЃЈ
Ђк MЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнвбжЊЧѓЕуAЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЂйИљОнAЃЈЉ2ЃЌ6ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌЧѓЕУABЕФНтЮіЪНЮЊЃКy=Љ2x+2ЃЌЩшPЃЈaЃЌЉa2Љ3a+4ЃЉЃЌдђEЃЈaЃЌЉ2a+2ЃЉЃЌРћгУPE=Љa2Љ3a+4Љ(Љ2a+2)=Љ(a+![]() )2+
)2+![]() ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯёгыаджЪМДЧѓНтЃЛ
ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯёгыаджЪМДЧѓНтЃЛ
ЂкИљОнЕуMдквдABЮЊжБОЖЕФдВЩЯЃЌЕУЕНЁЯAMB=90ЁуЃЌМДAM2+BM2=AB2![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌ
ЃЌ![]() ЃЌAB2ЙЪПЩСаГіЗНГЬЧѓНт.
ЃЌAB2ЙЪПЩСаГіЗНГЬЧѓНт.
НтЃКЃЈ1ЃЉЁпBЃЈ1ЃЌ0ЃЉ
ЁрOB=1ЃЌ
ЁпOC=2OB=2ЃЌ
ЁрBC=3 ,CЃЈЉ2ЃЌ0ЃЉ
RtЁїABCжаЃЌtanЁЯABC=2ЃЌ
Ёр![]() =2ЃЌ
=2ЃЌ
ЁрAC=6ЃЌ
ЁрAЃЈЉ2ЃЌ6ЃЉЃЌ
АбAЃЈЉ2ЃЌ6ЃЉКЭBЃЈ1ЃЌ0ЃЉДњШыy=Љx2+bx+cЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКy=Љx2Љ3x+4ЃЛ
ЃЈ2ЃЉЂйЁпAЃЈЉ2ЃЌ6ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌ
взЕУABЕФНтЮіЪНЮЊЃКy=Љ2x+2ЃЌ
ЩшPЃЈaЃЌЉa2Љ3a+4ЃЉЃЌдђEЃЈaЃЌЉ2a+2ЃЉЃЌ
ЁрPE=Љa2Љ3a+4Љ(Љ2a+2)=Љa2Љa+2=Љ(a+![]() )2+
)2+![]()
ЁрЕБa=![]() ЪБЃЌPE
ЪБЃЌPE![]() =
=![]() ,ДЫЪБP(
,ДЫЪБP(![]() ,
,![]() )
)
ЂкЁпMдкжБЯпPDЩЯЃЌЧвP(![]() ,
,![]() )ЃЌ
)ЃЌ
![]()
Ёр
![]() +
+![]()
AB2=32+62=45ЃЌ
ЁпЕуMдквдABЮЊжБОЖЕФдВЩЯ
ДЫЪБЁЯAMB=90ЁуЃЌ
ЁрAM2+BM2=AB2ЃЌ
Ёр +
+![]() +
+![]() =45
=45
НтЕУЃК![]() ,
,![]()
ЁрMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() гы
гы![]() гЫНЛгк
гЫНЛгк![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЖЅЕуЮЊ
ЃЌЖЅЕуЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєНЋХзЮяЯп![]() би
би![]() жсЦНвЦКѓЕУЕНХзЮяЯп
жсЦНвЦКѓЕУЕНХзЮяЯп![]() ЃЌХзЮяЯп
ЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() Чвгы
Чвгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЖЅЕуЮЊ
ЃЌЖЅЕуЮЊ![]() ЃЎдкХзЮяЯп
ЃЎдкХзЮяЯп![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЪЙ
ЪЙ![]() ЃПШєДцдкЃЌЧѓГіЕу
ЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§yЃНax2+bx+cЃЈaЁй0ЃЉЕФВПЗжЭМЯѓШчЭМЃЌЭМЯѓЙ§ЕуЃЈЉ1ЃЌ0ЃЉЃЌЖдГЦжсЮЊжБЯпxЃН2ЃЌЯТСаНсТлЃК
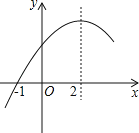
Ђй4a+bЃН0ЃЛЂк9a+cЃО3bЃЛЂл,3a+cЃО0ЃЛЂмЕБxЃОЉ1ЪБЃЌyЕФжЕЫцxжЕЕФдіДѓЖјдіДѓЃЎЂн![]() ЃЈmЮЊШЮвтЪЕЪ§ЃЉЦфжае§ШЗЕФНсТлга_____ЃЎЃЈЬюађКХЃЉ
ЃЈmЮЊШЮвтЪЕЪ§ЃЉЦфжае§ШЗЕФНсТлга_____ЃЎЃЈЬюађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЪЧЁЯBACЕФЦНЗжЯпЃЌОЙ§
ЪЧЁЯBACЕФЦНЗжЯпЃЌОЙ§![]() ЁЂ
ЁЂ![]() СНЕуЕФдВЕФдВаФ
СНЕуЕФдВЕФдВаФ![]() ЧЁКУТфдк
ЧЁКУТфдк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЗжБ№гы
ЗжБ№гы![]() ЁЂ
ЁЂ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЁЂ
ЁЂ![]() .
.
ЃЈ1ЃЉХаЖЯжБЯп![]() гы
гы![]() ЕФЮЛжУЙиЯЕВЂжЄУїЃЛ
ЕФЮЛжУЙиЯЕВЂжЄУїЃЛ
ЃЈ2ЃЉШє![]() ЕФАыОЖЮЊ2ЃЌ
ЕФАыОЖЮЊ2ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЖШ.
ЕФГЄЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
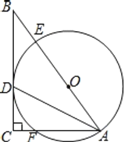
ЁОЬтФПЁПШчЭМЫљЪОЃЌАыдВOЕФжБОЖABЃН4ЃЌ![]() ЃН
ЃН![]() ЃЌDEЁЭABгкEЃЌDFЁЭACгкFЃЌСЌНгCDЃЌDBЃЌODЃЎ
ЃЌDEЁЭABгкEЃЌDFЁЭACгкFЃЌСЌНгCDЃЌDBЃЌODЃЎ
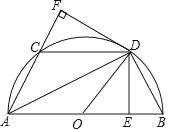
ЃЈ1ЃЉЧѓжЄЃКЁїCDFЁеЁїBDEЃЛ
ЃЈ2ЃЉЕБADЃНЁЁ ЁЁЪБЃЌЫФБпаЮAODCЪЧСтаЮЃЛ
ЃЈ3ЃЉЕБADЃНЁЁ ЁЁЪБЃЌЫФБпаЮAEDFЪЧе§ЗНаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌACЪЧЁбOЕФжБОЖЃЌBCЪЧЁбOЕФЯвЃЌЕуPЪЧЁбOЭтвЛЕуЃЌСЌНгPAЃЌPBЃЌABЃЌвбжЊЁЯPBA=ЁЯCЃЎ

ЃЈ1ЃЉЧѓжЄЃКPBЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгOPЃЌШєOPЁЮBCЃЌЧвOP=8ЃЌЁбOЕФАыОЖЮЊ![]() ЃЌЧѓBCЕФГЄЃЎ
ЃЌЧѓBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙмжаЗХжУзХШ§ИљЭЌбљЕФЩўзгAA1ЁЂBB1ЁЂCC1ЃЛ
ЃЈ1ЃЉаЁУїДгетШ§ИљЩўзгжаЫцЛњбЁвЛИљЃЌЧЁКУбЁжаЩўзгAA1ЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉаЁУїЯШДгзѓЖЫAЁЂBЁЂCШ§ИіЩўЭЗжаЫцЛњбЁСНИіДђвЛИіНсЃЌдйДггвЖЫA1ЁЂB1ЁЂC1Ш§ИіЩўЭЗжаЫцЛњбЁСНИіДђвЛИіНсЃЌЧѓетШ§ИљЩўзгФмСЌНсГЩвЛИљГЄЩўЕФИХТЪЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌMЃЌNЪЧвдABЮЊжБОЖЕФЁбOЩЯЕФЕуЃЌЧв![]() ЃН
ЃН![]() ЃЌЯвMNНЛABгкЕуCЃЌBMЦНЗжЁЯABDЃЌMFЁЭBDгкЕуFЃЎ
ЃЌЯвMNНЛABгкЕуCЃЌBMЦНЗжЁЯABDЃЌMFЁЭBDгкЕуFЃЎ
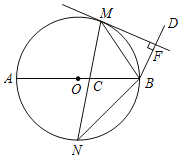
ЃЈ1ЃЉЧѓжЄЃКMFЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєCNЃН3ЃЌBNЃН4ЃЌЧѓCMЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB=60ЁуЃЌAC=1ЃЌDЪЧБпABЕФжаЕуЃЌEЪЧБпBCЩЯвЛЕуЃЌШєDEЦНЗжЁїABCЕФжмГЄЃЌдђDEЕФГЄЪЧЃЈ ЃЉ
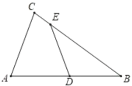
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com