
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
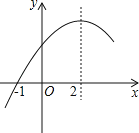
①4a+b=0;②9a+c>3b;③,3a+c>0;④当x>﹣1时,y的值随x值的增大而增大.⑤![]() (m为任意实数)其中正确的结论有_____.(填序号)
(m为任意实数)其中正确的结论有_____.(填序号)
【答案】①③⑤
【解析】
由抛物线的对称轴方程得到b=-4a>0,则可对①进行判断;由于x=-3时,y<0,则可对②进行判断;利用抛物线与x轴的一个交点为(-1,0)得a-b+c=0,把b=-4a代入可得3a+c=-2a,结合a<0,于是可对③进行判断;根据二次函数图象的对称轴与函数的性质可对④进行判断;通过![]() ≤0,可判断⑤.
≤0,可判断⑤.
∵抛物线的对称轴为直线x=![]() =2,
=2,
∴b=4a,即4a+b=0,所以①正确;
∵x=3时,y<0,
∴9a3b+c<0,即9a+c<3b,所以②错误;
∵抛物线与x轴的一个交点为(1,0),
∴x=1时,ab+c=0,
∴a+4a+c=0,
∴3a+c=-2a,
∵a<0,
∴3a+c=-2a>0,所以③正确;
∵抛物线的对称轴为直线x=2,开口向下,
∴当-1<x<2时,函数值随x增大而增大,所以④错误;
∵b=4a,
∴![]() =
=![]() ,
,
∴![]() ,∴⑤正确.
,∴⑤正确.
故答案为①③⑤.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 交y轴于点A(0,4),交x轴于点B(4,0)、C,点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作
交y轴于点A(0,4),交x轴于点B(4,0)、C,点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作![]() 于点Q,连接AP(AP不平行x轴).
于点Q,连接AP(AP不平行x轴).
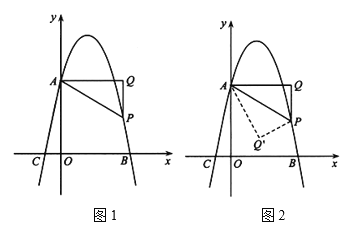
(1)求抛物线的解析式;
(2)点P在抛物线上运动,若![]() ∽
∽![]() (点P与点C对应),求点P的坐标;
(点P与点C对应),求点P的坐标;
(3)如图2,若点P位于抛物线的对称轴的右侧,将![]() 沿AP对折,点Q的对应点为点
沿AP对折,点Q的对应点为点![]() ,当点
,当点![]() 落在x轴上时,求点P的坐标.
落在x轴上时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的众数和中位数分别是( )
A.100,10B.10,20C.17,10D.17,20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(注:凸四边形就是没有角度数大于180°的四边形,把四边形的任何一边向两方延长,其他各边都在延长所得直线的同一旁,这样的四边形叫做凸四边形.)

(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有_________;②在凸四边形![]() 中,
中,![]() 且
且![]() ,则该四边形_________“十字形”.(填“是”或“不是”)
,则该四边形_________“十字形”.(填“是”或“不是”)
(2)如图1,![]() ,
,![]() ,
,![]() ,
,![]() 是半径为1的
是半径为1的![]() 上按逆时针方向排列的四个动点,
上按逆时针方向排列的四个动点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)如图2,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (
(![]() ,
,![]() ,
,![]() 为常数,
为常数,![]() ,
,![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 是抛物线与
是抛物线与![]() 轴的交点,点
轴的交点,点![]() 的坐标为
的坐标为![]() ,记“十字形”
,记“十字形”![]() 的面积为
的面积为![]() ,记
,记![]() ,
,![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,
,![]() .求同时满足下列三个条件的抛物线的解析式:①
.求同时满足下列三个条件的抛物线的解析式:①![]() ;②
;②![]() ;③“十字形”
;③“十字形”![]() 的周长为
的周长为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
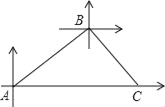
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
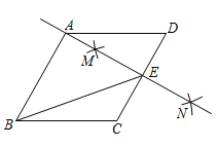
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
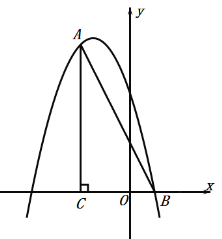
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.
①求点P的坐标和PE的最大值.
②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是被誉为“川北第一楼”的凤凰楼,它不仅是广元市的城标,更是一份承传文化的载体.李铭和王华同学想借助无人机测量凤凰楼的高度,如图②为测量示意图,他们站在坡度是![]() ,坡面长为
,坡面长为![]() 的斜坡
的斜坡![]() 的坡底
的坡底![]() 处操控无人机,无人机从坡顶
处操控无人机,无人机从坡顶![]() 出发,以
出发,以![]() 的速度,沿仰角
的速度,沿仰角![]() 的方向爬升,
的方向爬升,![]() 时到达空中的
时到达空中的![]() 处.
处.
(1)求此时无人机离坡底![]() 所在地面的高度;
所在地面的高度;
(2)如图②,无人机在![]() 处测得凤凰楼顶部
处测得凤凰楼顶部![]() 的仰角为
的仰角为![]() ,底部
,底部![]() 的俯角为
的俯角为![]() (凤凰楼与李铭和王华所站坡底
(凤凰楼与李铭和王华所站坡底![]() 在同一水平面),求凤凰楼的高度
在同一水平面),求凤凰楼的高度![]() .
.
(结果精确到![]() ;参考数据:
;参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
图① 图②
图②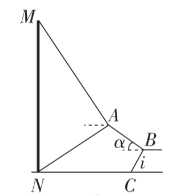
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com