
【题目】如图所示,半圆O的直径AB=4,![]() =
=![]() ,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
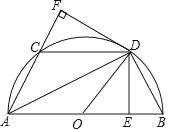
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
【答案】(1)证明见解析;(2)2![]() ;(3))2
;(3))2![]() .
.
【解析】
(1)根据角平分线的性质,可得DF与DE的关系,根据圆周角定理,可得DC与DB的关系,再根据HL,即可证明;(2)根据菱形的性质,可得OD与CD,OD与BD的关系,根据等边三角形的性质,可得∠DBA的度数,根据三角函数值,即可求解;(3)根据圆周角定理,可得OD⊥AB,根据勾股定理,即可求出AD的长.
(1)证明:∵![]() ,
,
∴CD=BD,∠FAD=∠BAD.
∵DF⊥AC,DE⊥AB,
∴DF=DE,∠BED=∠CFD=90°.
在Rt△CFD和Rt△BED中,![]()
∴△CDF≌△BDE(HL).
(2)四边形AODC是菱形时,
OD=CD=BD=OB,
∴∠DBA=60°,
∴AD=AB·sin∠DBA=4sin60°=2![]() .
.
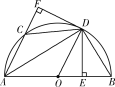
(3)当OD⊥AB,即OD与OE重合时,四边形AEDF是正方形,
由勾股定理得
AD=![]() =2
=2![]() .
.


科目:初中数学 来源: 题型:
【题目】我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(注:凸四边形就是没有角度数大于180°的四边形,把四边形的任何一边向两方延长,其他各边都在延长所得直线的同一旁,这样的四边形叫做凸四边形.)

(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有_________;②在凸四边形![]() 中,
中,![]() 且
且![]() ,则该四边形_________“十字形”.(填“是”或“不是”)
,则该四边形_________“十字形”.(填“是”或“不是”)
(2)如图1,![]() ,
,![]() ,
,![]() ,
,![]() 是半径为1的
是半径为1的![]() 上按逆时针方向排列的四个动点,
上按逆时针方向排列的四个动点,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
(3)如图2,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() (
(![]() ,
,![]() ,
,![]() 为常数,
为常数,![]() ,
,![]() )与
)与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 是抛物线与
是抛物线与![]() 轴的交点,点
轴的交点,点![]() 的坐标为
的坐标为![]() ,记“十字形”
,记“十字形”![]() 的面积为
的面积为![]() ,记
,记![]() ,
,![]() ,
,![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() ,
,![]() ,
,![]() .求同时满足下列三个条件的抛物线的解析式:①
.求同时满足下列三个条件的抛物线的解析式:①![]() ;②
;②![]() ;③“十字形”
;③“十字形”![]() 的周长为
的周长为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
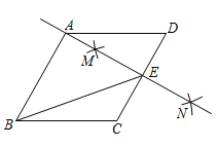
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
按逆时针方向旋转,得到![]() .
.
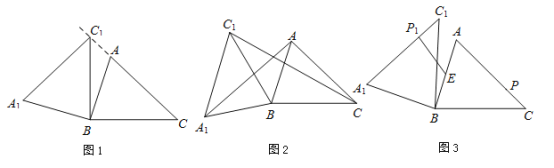
(1)如图1,当点![]() 在线段
在线段![]() 的延长线上时,求
的延长线上时,求![]() 的度数;
的度数;
(2)如图2,连接![]() ,
,![]() .若
.若![]() 的面积为4,求
的面积为4,求![]() 的面积;
的面积;
(3)如图3,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转过程中,点
按逆时针方向旋转过程中,点![]() 的对应点是点
的对应点是点![]() ,求线段
,求线段![]() 长度的最小值.
长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
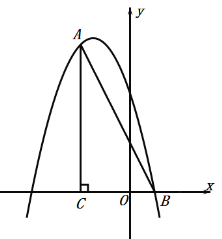
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.
①求点P的坐标和PE的最大值.
②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为![]() 的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
的等边三角形.将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
(1)如图a,当θ=20°时,判断△ABD与△ACE是否全等?并说明理由;
(2)当△ABC旋转到如图b所在位置时(60°<θ<120°),求∠BOE的度数;
(3)在θ从60°到120°的旋转过程中,点O运动的轨迹长为 .


查看答案和解析>>
科目:初中数学 来源: 题型:
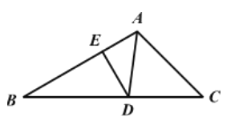
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )
A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解“停课不停学”期间,学生对线上学习方式的偏好情况,某校随机拍取40名学生进行问卷调查,其统计结果如表:
最喜欢的线上学习方式(没人最多选一种) | 人数 |
直播 | 10 |
录播 |
|
资源包 | 5 |
线上答疑 | 8 |
合计 | 40 |
(1)![]() ;
;
(2)若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图,求“直播"对应扇形的圆心角度数;
(3)根据调查结果估计该校10000名学生中,最喜欢“线上答疑”的学生人数;
(4)在最喜欢“资源包”的学生中,有2名男生,3名女生.现从这5名学生中随机抽取2名学生介绍学习经验,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com