
【题目】为了解“停课不停学”期间,学生对线上学习方式的偏好情况,某校随机拍取40名学生进行问卷调查,其统计结果如表:
最喜欢的线上学习方式(没人最多选一种) | 人数 |
直播 | 10 |
录播 |
|
资源包 | 5 |
线上答疑 | 8 |
合计 | 40 |
(1)![]() ;
;
(2)若将选取各种“最喜欢的线上学习方式”的人数所占比例绘制成扇形统计图,求“直播"对应扇形的圆心角度数;
(3)根据调查结果估计该校10000名学生中,最喜欢“线上答疑”的学生人数;
(4)在最喜欢“资源包”的学生中,有2名男生,3名女生.现从这5名学生中随机抽取2名学生介绍学习经验,求恰好抽到1名男生和1名女生的概率.
【答案】(1)17;(2)“直播”所占扇形圆心角度数为90°;(3)估计该校最喜难“线上答疑”的学生人数为200人;(4)恰好抽得一男一女的概率为![]() .
.
【解析】
(1)根据四种学习方式的人数之和等于40可求出a的值;
(2)用360°乘以最喜欢的线上学习方式是直播的人数所占比例可得;
(3)用总人数乘以样本中最喜欢“线上答疑”的学生人数所占比例可得答案;
(4)画树状图展示所有20种等可能的结果数,再找出恰好抽到1名男生和1名女生的结果数,然后利用概率公式求解.
(1)a=40-(10+5+8)=17,
故答案为:17;
(2)“直播”所占扇形圆心角度数为:![]() .
.
答:“直播”所占扇形圆心角度数为:90°.
(3)最喜欢“线上答疑”的学生人数:![]() .
.
答:估计该校最喜难“线上答疑”的学生人数为200人.
(4)设最喜欢“资源包”的学生中,将男生记为![]() ,
,![]() ,女生记为
,女生记为![]() ,
,![]() ,
,![]() .
.

由树状图可知,共有20种等可能的结果,其中恰好一男一女的有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共12种.
共12种.
所以恰好抽得一男一女的概率为:![]() .
.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,半圆O的直径AB=4,![]() =
=![]() ,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
,DE⊥AB于E,DF⊥AC于F,连接CD,DB,OD.
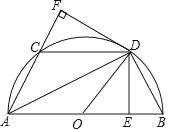
(1)求证:△CDF≌△BDE;
(2)当AD= 时,四边形AODC是菱形;
(3)当AD= 时,四边形AEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2 、O3…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2020秒时,点P的坐标是__________________.
个单位长度,则第2020秒时,点P的坐标是__________________.
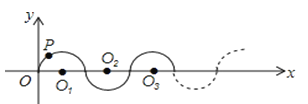
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
![]() 如图1,点
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
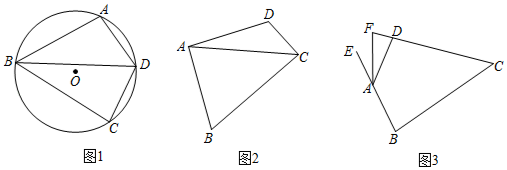
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点,若DE平分△ABC的周长,则DE的长是( )
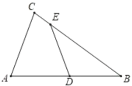
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小明在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线相互垂直的三角形“中垂三角形”,如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AM⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
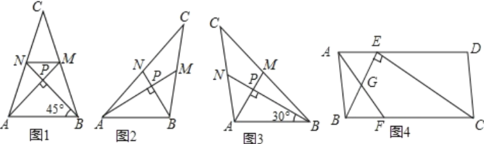
(特例研究)
(1)如图1,当tan∠PAB=1,c=4![]() 时,a=b= ;
时,a=b= ;
(归纳证明)
(2)请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图2证明你的结论;
(拓展证明)
(3)如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF交BE相较于点G,AD=3![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com