【题目】数学课上，李老师准备了四张背面都一样的卡片A、B、C、D，每张卡片的正面标有字母a、b、c表示三条线段（如下图）．把四张卡片背面朝上放在桌面上，李老师从这四张卡片中随机抽取一张卡片后不放回，再随机抽取一张．
⑴ 李老师随机抽取一张卡片，抽到卡片B的概率等于 ；
⑵ 求李老师抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率．
科目：初中数学 来源： 题型：
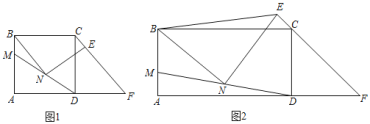
【题目】在矩形ABCD中，点F在AD延长线上，且DF＝DC，M为AB边上一点，N为MD的中点，点E在直线CF上，且BN＝NE．
（1）如图1，若AB＝BC＝6，BM＝
AB，E为线段FC上的点，试求NE的长；
（2）如图2，若AB＜BC，E为线段FC延长线上的点，连结BE，求证：BE＝
NE．
查看答案和解析>>
科目：初中数学 来源： 题型：
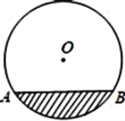
【题目】某居民小区的一处圆柱形输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径．如图，输水管道有水部分的水面宽AB=16cm，水最深的地方的高度为4cm，则这个圆形截面的半径为________cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
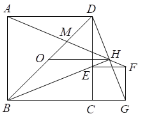
【题目】如图，四边形ABCD、CEFG都是正方形，E在CD上且BE平分∠DBC，O是BD中点，直线BE、DG交于H．BD，AH交于M，连接OH，下列四个结论：
① BE⊥GD； ② OH＝
BG； ③ ∠AHD＝45°； ④ GD＝
AM．
其中正确的结论个数有
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
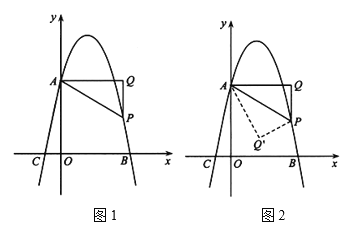
【题目】如图1，已知抛物线
交y轴于点A（0，4），交x轴于点B（4，0）、C，点P是抛物线上一动点，过点P作x轴的垂线PQ，过点A作
于点Q，连接AP（AP不平行x轴）．
（1）求抛物线的解析式；
（2）点P在抛物线上运动，若
∽
（点P与点C对应），求点P的坐标；
（3）如图2，若点P位于抛物线的对称轴的右侧，将
沿AP对折，点Q的对应点为点
，当点落在x轴上时，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】正方形
、正方形
如图放置，点
在同一条直线上，点
在
边上，
，且
，连结
交
于
，有下列结论：①
；②
；③
；④
；⑤
．以上结论正确的个数有( )
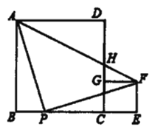
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们不妨约定：对角线互相垂直的凸四边形叫做“十字形”．（注：凸四边形就是没有角度数大于180°的四边形，把四边形的任何一边向两方延长，其他各边都在延长所得直线的同一旁，这样的四边形叫做凸四边形．）
（1）①在“平行四边形，矩形，菱形，正方形”中，一定是“十字形”的有_________；②在凸四边形
中，
且
，则该四边形_________“十字形”．（填“是”或“不是”）
（2）如图1，
，
，
，
是半径为1的
上按逆时针方向排列的四个动点，
与
交于点
，
，当
时，求
的取值范围；
（3）如图2，在平面直角坐标系
中，抛物线
（
，
，
为常数，
，
）与
轴交于，两点（点在点的左侧），是抛物线与
轴的交点，点的坐标为
，记“十字形”的面积为
，记
，
，
，
的面积分别为
，
，
，
．求同时满足下列三个条件的抛物线的解析式：①
；②
；③“十字形”的周长为
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC是边长为
的等边三角形．将△ABC绕点A逆时针旋转角θ（0°＜θ＜180°），得到△ADE，BD和EC所在直线相交于点O．
（1）如图a，当θ=20°时，判断△ABD与△ACE是否全等？并说明理由；
（2）当△ABC旋转到如图b所在位置时（60°＜θ＜120°），求∠BOE的度数；
（3）在θ从60°到120°的旋转过程中，点O运动的轨迹长为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
