
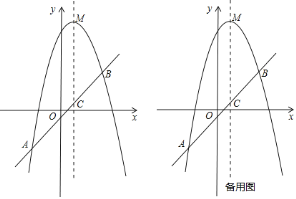
【题目】已知,如图,抛物线![]() 的顶点为
的顶点为![]() ,经过抛物线上的两点
,经过抛物线上的两点![]() 和
和![]() 的直线交抛物线的对称轴于点
的直线交抛物线的对称轴于点![]() .
.
(1)求抛物线的解析式和直线![]() 的解析式.
的解析式.
(2)在抛物线上![]() 两点之间的部分(不包含
两点之间的部分(不包含![]() 两点),是否存在点
两点),是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若点![]() 在抛物线上,点
在抛物线上,点![]() 在
在![]() 轴上,当以点
轴上,当以点![]() 为顶点的四边形是平行四边形时,直接写出满足条件的点
为顶点的四边形是平行四边形时,直接写出满足条件的点![]() 的坐标.
的坐标.
【答案】(1)抛物线的表达式为:![]() ,直线
,直线![]() 的表达式为:
的表达式为:![]() ;(2)存在,理由见解析;点
;(2)存在,理由见解析;点![]()
![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)二次函数表达式为:y=a(x-1)2+9,即可求解;
(2)S△DAC=2S△DCM,则![]() ,,即可求解;
,,即可求解;
(3)分AM是平行四边形的一条边、AM是平行四边形的对角线两种情况,分别求解即可.
解:(1)二次函数表达式为:![]() ,
,
将点![]() 的坐标代入上式并解得:
的坐标代入上式并解得:![]() ,
,
故抛物线的表达式为:![]() …①,
…①,
则点![]() ,
,
将点![]() 的坐标代入一次函数表达式并解得:
的坐标代入一次函数表达式并解得:
直线![]() 的表达式为:
的表达式为:![]() ;
;
(2)存在,理由:
二次函数对称轴为:![]() ,则点
,则点![]() ,
,
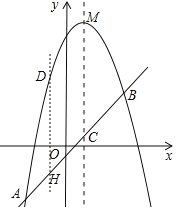
过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,
,
设点![]() ,点
,点![]() ,
,
∵![]() ,
,
则![]() ,
,
解得:![]() 或5(舍去5),
或5(舍去5),
故点![]() ;
;
(3)设点![]() 、点
、点![]() ,
,![]() ,
,
①当![]() 是平行四边形的一条边时,
是平行四边形的一条边时,
点![]() 向左平移4个单位向下平移16个单位得到
向左平移4个单位向下平移16个单位得到![]() ,
,
同理,点![]() 向左平移4个单位向下平移16个单位为
向左平移4个单位向下平移16个单位为![]() ,即为点
,即为点![]() ,
,
即:![]() ,
,![]() ,而
,而![]() ,
,
解得:![]() 或﹣4,
或﹣4,
故点![]() 或
或![]() ;
;
②当![]() 是平行四边形的对角线时,
是平行四边形的对角线时,
由中点公式得:![]() ,
,![]() ,而
,而![]() ,
,
解得:![]() ,
,
故点![]() 或
或![]() ;
;
综上,点![]() 或
或![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
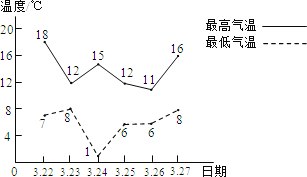
【题目】如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况.
(1)最低气温的中位数是 ℃;3月24日的温差是 ℃;
(2)分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;
(3)经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校计划举行社会实践活动,现随机抽取了部分学生进行主题为“你最想去的地点是?”的问卷调查,要求学生必须从“A(大鹏所城),B(园山),C(西冲),D(欢乐谷)”四个景点中选择一项,根据调查结果,绘制了如图两幅不完整的统计图,请你根据图中所提供的信息,完成下列问题:
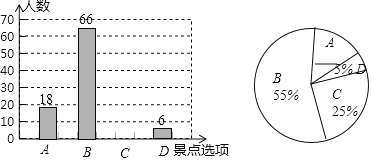
(1)本次调查的学生人数为 人;
(2)在扇形统计图中,“园山”部分所占圆心角的度数为 ;
(3)请将两幅统计图补充完整;
(4)若该校共有3000名学生,估计该校最想去大鹏所城的学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
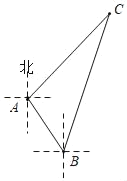
【题目】如图,某考察船在某海域进行科考活动,在点A测得小岛C在它的东北方向上,它沿南偏东37°方向航行了2海里到达点B处,又测得小岛C在它的北偏东23°方向上.
(1)求∠C的度数;
(2)求该考察船在点B处与小岛C之间的距离.(精确到0.1海里)
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
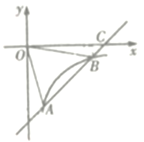
【题目】如图,已知一次函数y= kx +b的图象交反比例函数![]() 的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
(1)求这两个函数的解析式;
(2)连接QA、OB.求△AOB的面积;
(3)请直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
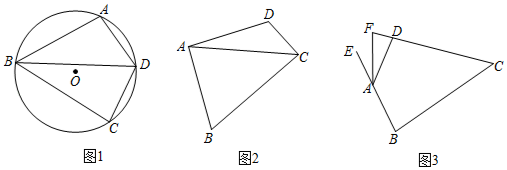
![]() 如图1,点
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
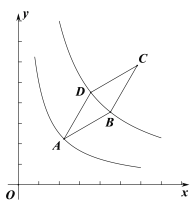
【题目】如图所示,菱形ABCD的顶点A在反比例函数y=![]() (x>0)的图象上,函数y=
(x>0)的图象上,函数y=![]() (k>5,x>0)的图象关于直线AC对称,且经过点B、D两点.若AB=2,∠DAB=30°,如下结论:①O、A、C三点在同一直线上;②点A的横坐标是
(k>5,x>0)的图象关于直线AC对称,且经过点B、D两点.若AB=2,∠DAB=30°,如下结论:①O、A、C三点在同一直线上;②点A的横坐标是![]() ;③点D的坐标是(
;③点D的坐标是(![]() +1,2
+1,2![]() );④比例系数k的值为10+
);④比例系数k的值为10+![]() .其中不正确的结论是( )
.其中不正确的结论是( )
A.①②③B.②③④C.①③④D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com