
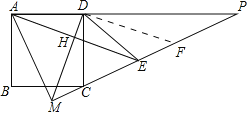
【题目】如图,正方形ABCD的边长为![]() ,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是____________
,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是____________

①∠DAE=∠DEA;②∠DMC=45°;③![]() ;④若MH=2,则S△CMD=
;④若MH=2,则S△CMD=![]()
【答案】①②③
【解析】
①利用等腰三角形的性质即可证明.
②根据DA=DC=DE,利用圆周角定理可知∠AEC=![]() ∠ADC=45°,即可解决问题.
∠ADC=45°,即可解决问题.
③如图,作DF⊥DM交PM于F,证明△ADM≌△CDF(SAS)即可解决问题.
④解直角三角形求出CE=EF=![]() 可得结论.
可得结论.
解:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵DC=DE, ∴DA=DE, ∴∠DAE=∠DEA,故①正确,
∵DA=DC=DE,
![]() 在以
在以![]() 为圆心,
为圆心,![]() 为半径的圆上,
为半径的圆上,
∴∠AEC=![]() ∠ADC=45°(圆周角定理),
∠ADC=45°(圆周角定理),
∵DM⊥AE, ∴∠EHM=90°, ∴∠DMC=45°,故②正确,
如图,作DF⊥DM交PM于F,
∵∠ADC=∠MDF=90°,
∴∠ADM=∠CDF,
∵∠DMF=45°,
∴∠DMF=∠DFM=45°,
∴DM=DF,
∵DA=DC,
∴△ADM≌△CDF(SAS),
∴AM=CF,
∴AM+CM=CF+CM=MF=![]() DM,
DM,
∴ ![]() ,故③正确,
,故③正确,
![]()
![]()
![]() MH=2,
MH=2,
![]() AH=MH=HE=2,AM=EM=
AH=MH=HE=2,AM=EM=![]()
在Rt△ADH中,DH=![]()
∴DM=3,AM+CM=![]()
∴CM=CE=![]()
∴S△DCM=S△DCE,
故④错误.
故答案①②③.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】现有A、B两个不透明袋子,分别装有3个除颜色外完全相同的小球。其中,A袋装有2个白球,1个红球;B袋装有2个红球,1个白球。
(1)将A袋摇匀,然后从A袋中随机取出一个小球,求摸出小球是白色的概率;
(2)小华和小林商定了一个游戏规则:从摇匀后的A,B两袋中随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜。请用列表法或画出树状图的方法说明这个游戏规则对双方是否公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
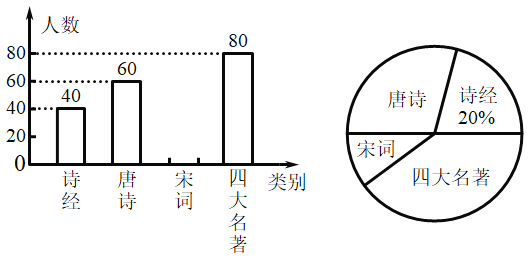
【题目】某校开展诵读“诗经、唐诗、宋词、四大名著”的活动,为了解学生对着四项诵读内容的喜爱程度,在全校学生中随机抽取部分学生进行问卷调查(在这四项诵读内容中,被调查的学生必须满足且只能选择一项)将收集的数据进行整理,并绘制了两幅不完整的统计图(如图)请跟进图中提供的信息,回答以下问题:
(1)本次调查中,随机抽取的学生有__________人,其中喜爱诵读|宋词的有___________人.
(2)补全条形统计图;
(3)若该校有2000名学生,估计全校学生中约有多少人喜爱诵读|宋词?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
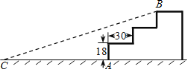
A.270cmB.210cmC.180cmD.96cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,P为BA延长线上一点,点C在⊙O上,连接PC,D为半径OA上一点,PD=PC,连接CD并延长交⊙O于点E,且E是![]() 的中点.
的中点.
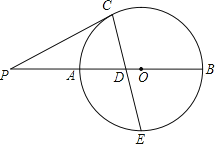
(1)求证:PC是⊙O的切线;
(2)若AB=8,CDDE=15,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,矩形
,矩形![]() 在直线
在直线![]() 上绕其右下角的顶点
上绕其右下角的顶点![]() 向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转100次后顶点
向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转100次后顶点![]() 在整个旋转过程中所经过的路程之和是_________.
在整个旋转过程中所经过的路程之和是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
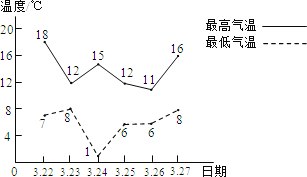
【题目】如图所示为3月22日至27日间,我区每日最高气温与最低气温的变化情况.
(1)最低气温的中位数是 ℃;3月24日的温差是 ℃;
(2)分别求出3月22日至27日间的最高气温的平均数、最低气温的平均数;
(3)经过计算,最高气温和最低气温的方差分别为6.33、5.67,数据更稳定的是最高气温还是最低气温?
查看答案和解析>>
科目:初中数学 来源: 题型:
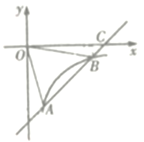
【题目】如图,已知一次函数y= kx +b的图象交反比例函数![]() 的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
(1)求这两个函数的解析式;
(2)连接QA、OB.求△AOB的面积;
(3)请直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com