
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
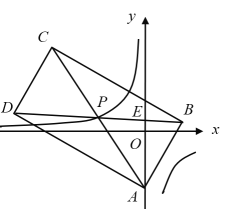
(1)求![]() 的值;
的值;
(2)若将矩形![]() 向下平移
向下平移![]() 个单位,使点
个单位,使点![]() 落在反比例函数
落在反比例函数![]() 的图象上,求
的图象上,求![]() 的值;
的值;
(3)求![]() 的值.
的值.
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段![]() 上任取一点
上任取一点![]() ,将线段
,将线段![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,将线段
,将线段![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .直线
.直线![]() 分别交
分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,有下列结论:①
两点,有下列结论:①![]() ;②四边形
;②四边形![]() 为平行四边形;③
为平行四边形;③![]() ;④
;④![]() .其中正确的结论是( )
.其中正确的结论是( )
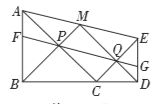
A.①③④B.①②③C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)求该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,房间数大大增加.每间客房收费20钱,且每间客房最多入住4人,一次性定客房18间以上(含18间),房费按8折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知有一种键盘密码,每个字母与所在按键的数字序号对应(见如图),如字母![]() 与数字序号0对应,当明文中的字母对应的序号为
与数字序号0对应,当明文中的字母对应的序号为![]() 时,将
时,将![]() 除以26后所得的余数作为密文中的字母对应的序号,例如明文“
除以26后所得的余数作为密文中的字母对应的序号,例如明文“![]() ”对应密文“
”对应密文“![]() ”
”
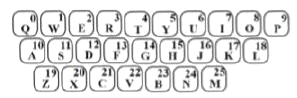
按上述规定,将密文“![]() ” 解密成明文后是( )
” 解密成明文后是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,AD=AE,∠B=∠ACE,且B、C、D三点在一条直线上,
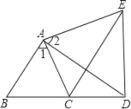
(1)试说明△ABD与△ACE全等的理由;
(2)如果∠B=60°,试说明线段AC、CE、CD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有以下命题:
①如果三角形的三个内角的度数比是![]() ,那么这个三角形是直角三角形;
,那么这个三角形是直角三角形;
②如果不等式![]() 的解集为
的解集为![]() ,那么
,那么![]() ;
;
③若将一次函数![]() 的图象向上平移3个单位,则平移所得直线不经过第四象限;
的图象向上平移3个单位,则平移所得直线不经过第四象限;
④命题“对角线互相垂的四边形是菱形”的逆命题.
则真命题的个数为( ).
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.

(1)求反比例函数的解析式;
(2)求一次函数的解析式;
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com