
،¾جâؤ؟،؟بçح¼£¬إ×خïدكسëxضل½»سعA£¬Bء½µم£¬سëyضل½»سعµمC£¨0£¬©پ2£©£¬µمAµؤ×ّ±êتا£¨2£¬0£©£¬Pخھإ×خïدكةدµؤز»¸ِ¶¯µم£¬¹µمP×÷PD،حxضلسعµمD£¬½»ض±دكBCسعµمE£¬إ×خïدكµؤ¶ش³ئضلتاض±دكx£½©پ1£®
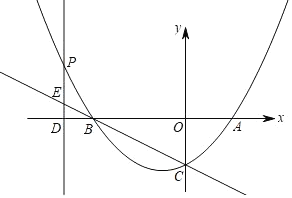
£¨1£©اَإ×خïدكµؤ؛¯ت±ي´ïت½£»
£¨2£©بôµمPشعµع¶دَدقؤع£¬ازPE£½![]() OD£¬اَ،÷PBEµؤأو»£®
OD£¬اَ،÷PBEµؤأو»£®
£¨3£©شع£¨2£©µؤجُ¼دآ£¬بôMخھض±دكBCةدز»µم£¬شعxضلµؤةد·½£¬تا·ٌ´وشعµمM£¬ت¹،÷BDMتازشBDخھرüµؤµبرüب½اذخ£؟بô´وشع£¬اَ³ِµمMµؤ×ّ±ê£»بô²»´وشع£¬اëثµأ÷ہيسة£®
،¾´ً°¸،؟£¨1£©y£½![]() x2+
x2+![]() x©پ2£»£¨2£©
x©پ2£»£¨2£©![]() £»£¨3£©M×ّ±êخھ£¨
£»£¨3£©M×ّ±êخھ£¨![]() £¬
£¬![]() £©»ٍ£¨©پ
£©»ٍ£¨©پ![]() £¬
£¬![]() £©£®
£©£®
،¾½âخِ،؟
£¨1£©µمA£¨2£¬0£©،¢µمB£¨-4£¬0£©£¬شٍ؛¯تµؤ±ي´ïت½خھ£؛y=a£¨x-2£©£¨x+4£©=a£¨x2+2x-8£©£¬¼´؟ةاَ½â£»
£¨2£©PE=![]() OD£¬شٍPE=£¨
OD£¬شٍPE=£¨![]() x2+
x2+![]() x-2-
x-2-![]() x+2£©=
x+2£©=![]() £¨-x£©£¬اَµأ£؛µمD£¨-5£¬0£©£¬ہûسأS،÷PBE=
£¨-x£©£¬اَµأ£؛µمD£¨-5£¬0£©£¬ہûسأS،÷PBE=![]() PE،ءBD=
PE،ءBD=![]() £¨
£¨![]() x2+
x2+![]() x-2-
x-2-![]() x+2£©£¨-4-x£©£¬¼´؟ةاَ½â£»
x+2£©£¨-4-x£©£¬¼´؟ةاَ½â£»
£¨3£©·ضء½ضضاé؟ِاَ½â¼´؟ة£؛¢ظµ±BD£½BMت±£¬¢عµ±BD£½DM£¨M،ن£©ت±£®
£¨1£©µمAµؤ×ّ±êتا£¨2£¬0£©£¬إ×خïدكµؤ¶ش³ئضلتاض±دكx£½©پ1£¬شٍµمB£¨©پ4£¬0£©£¬
شٍ؛¯تµؤ±ي´ïت½خھ£؛y£½a£¨x©پ2£©£¨x+4£©£½a£¨x2+2x©پ8£©£¬
°رµمC£¨0£¬-2£©´ْبëµأ£؛©پ8a£½©پ2£¬½âµأ£؛a£½![]() £¬
£¬
¹تإ×خïدكµؤ±ي´ïت½خھ£؛y£½![]() x2+
x2+![]() x©پ2£»
x©پ2£»
£¨2£©½«µمB،¢Cµؤ×ّ±ê´ْبëز»´خ؛¯ت±ي´ïت½£؛y£½mx+n²¢½âµأ£؛
ض±دكBCµؤ±ي´ïت½خھ£؛y£½©پ![]() x©پ2£¬شٍtan،دABC£½
x©پ2£¬شٍtan،دABC£½![]() £¬شٍsin،دABC£½
£¬شٍsin،دABC£½![]() £¬
£¬
ةèµمD£¨x£¬0£©£¬شٍµمP£¨x£¬![]() x2+
x2+![]() x©پ2£©£¬µمE£¨x£¬©پ
x©پ2£©£¬µمE£¨x£¬©پ![]() x©پ2£©£¬
x©پ2£©£¬
،كPE£½![]() OD£¬OD£½©پx£¬
OD£¬OD£½©پx£¬
،àPE£½£¨![]() x2+
x2+![]() x©پ2+
x©پ2+![]() x+2£©£½
x+2£©£½![]() x2+x£¬
x2+x£¬
¼´![]() x2+x=-
x2+x=-![]() x£¬
x£¬
½âµأ£؛x£½0»ٍ©پ5£¨ةلب¥x£½0£©£¬
¼´µمD£¨©پ5£¬0£©£¬
S،÷PBE£½![]() ،ءPE،ءBD£½
،ءPE،ءBD£½![]() £¨
£¨![]() x2+
x2+![]() x©پ2+
x©پ2+![]() x+2£©£¨©پ4©پx£©£½
x+2£©£¨©پ4©پx£©£½![]() £»
£»
£¨3£©سةجâزâµأ£؛،÷BDMتازشBDخھرüµؤµبرüب½اذخ£¬
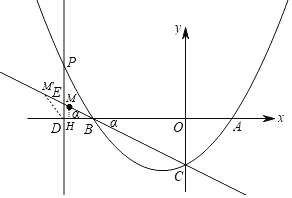
¢ظµ±BD£½BMت±£¬¹µمM×÷MH،حxضلسعµمH£¬
BD£½1£½BM£¬
شٍMH£½yM£½BMsin،دABC£½1،ء![]() £½
£½![]() £¬
£¬
شٍxM£½![]() £¬
£¬
¹تµمM£¨![]() £¬
£¬![]() £©£»
£©£»
¢عµ±BD£½DM£¨M،ن£©ت±£¬
ح¬ہي؟ةµأ£؛µمM،ن£¨©پ![]() £¬
£¬![]() £©£»
£©£»
¹تµمM×ّ±êخھ£¨©پ![]() £¬©پ
£¬©پ![]() £©»ٍ£¨©پ
£©»ٍ£¨©پ![]() £¬
£¬![]() £©£®
£©£®


 أûذ£؟خجأدµءذ´ً°¸
أûذ£؟خجأدµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ر§ذ£×éض¯ءثز»´خجهس²âتش£¬²âتشدîؤ؟سذA،°ء¢¶¨جّش¶،±،¢B،°ضہتµذؤاٍ،±،¢C،°رِخشئً×ّ،±،¢D،°100أ×إـ،±،¢E،°800أ×إـ،±£®¹و¶¨£؛أ؟أûر§ةْ²âتشبدئنضذA،¢Bخھ±ط²âدîؤ؟£¬µعبدîشعC،¢D،¢Eضذثو»ْ³éب،£¬أ؟دî10·ض£¨³ة¼¨¾ùخھصûتاز²»µحسع0·ض£©£®
£¨1£©حê³ةA،¢B±ط²âدîؤ؟؛َ£¬سأءذ±ي·¨£¬اَ¼×،¢ززء½ح¬ر§µعبدî³éب،²»ح¬دîؤ؟µؤ¸إآت£»
£¨2£©ؤ³°àسذ6أûؤذةْ³éµ½ءثE،°800أ×إـ،±دîؤ؟£¬ثûأاµؤ³ة¼¨·ض±ً£¨µ¥خ»£؛·ض£©خھ£؛x£¬6£¬7£¬8£¬8£¬9£®
¢ظزرضھصâ×é³ة¼¨µؤئ½¾ùت؛حضذخ»تدàµب£¬ازx²»تاصâ×é³ة¼¨ضذ×î¸كµؤ£¬شٍx= £»
¢ع¸أ°àر§ةْ±ûزٍ²،´ي¹ءث²âتش£¬²¹²â³éµ½ءثE،°800أ×إـ،±دîؤ؟£¬¼سةد±ûح¬ر§µؤ³ة¼¨؛َ£¬·¢دضصâ×é³ة¼¨µؤضعتسëضذخ»تدàµب£¬µ«ئ½¾ùت±بشہ´µؤئ½¾ùتذ،£¬شٍ±ûح¬ر§،°800أ×إـ،±µؤ³ة¼¨خھ¶àةظ£؟£»
¼× زز | |||
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ضذر§خھ·ل¸»ر§ةْµؤذ£ش°ةْ»î£¬×¼±¸ز»´خذش¹؛آٍبô¸ة¸ِ×ماٍ؛حہ؛اٍ£¨أ؟¸ِ×ماٍµؤ¼غ¸ٌدàح¬£¬أ؟¸ِہ؛اٍµؤ¼غ¸ٌدàح¬£©£¬بô¹؛آٍ3¸ِ×ماٍ؛ح2¸ِہ؛اٍ¹²ذè170شھ£¬¹؛آٍ2¸ِ×ماٍ؛ح5¸ِہ؛اٍ¹²ذè260شھ£®
£¨1£©¹؛آٍز»¸ِ×ماٍ،¢ز»¸ِہ؛اٍ¸÷ذè¶àةظشھ£؟£¨جلت¾£؛ءذ·½³ج×é½â´ً£©
£¨2£©¸ù¾ف¸أضذر§µؤتµ¼تاé؟ِ£¬ذèز»´خذش¹؛آٍ×ماٍ؛حہ؛اٍ¹²46¸ِ£¬زھاَ¹؛آٍ×ماٍ؛حہ؛اٍµؤ×ـ·رسأ²»³¬¹1480شھ£¬صâثùضذر§×î¶à؟ةزش¹؛آٍ¶àةظ¸ِہ؛اٍ£؟£¨جلت¾£؛ءذ²»µبت½½â´ً£©
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ذ،ءُ¶ش±¾°àح¬ر§µؤزµسàذثب¤°®؛أ½ّذذءثز»´خµ÷²é£¬ث¸ù¾ف²ة¼¯µ½µؤت¾ف£¬»وضئءثدآأوµؤح¼1؛حح¼2£®
اëؤم¸ù¾فح¼ضذجل¹©µؤذإد¢£¬½â´ًدآءذختجâ£؛
£¨1£©شعح¼1ضذ£¬½«،°تé»،±²؟·ضµؤح¼ذخ²¹³نحêصû£»
£¨2£©شعح¼2ضذ£¬اَ³ِ،°اٍہà،±²؟·ضثù¶شس¦µؤش²ذؤ½اµؤ¶بت£¬²¢·ض±ًذ´³ِ°®؛أ،°زôہض،±،¢،°تé»،±،¢،°ئنثü،±µؤبثتص¼±¾°àر§ةْتµؤ°ظ·ضت£»
£¨3£©¹غ²ىح¼1؛حح¼2£¬ؤمؤـµأ³ِؤؤذ©½لآغ£¨ض»زھذ´³ِز»جُ½لآغ£©£®


²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
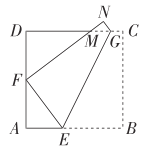
،¾جâؤ؟،؟بçح¼£¬شعص·½ذخABCDضذ£¬DC=8£¬دض½«ثؤ±كذخBEGCرطصغ؛غEG(G£¬E·ض±ًشعDC£¬AB±كةد)صغµ£¬ئن¶¥µمB£¬C·ض±ًآنشع±كADةد؛ح±كDCµؤةد²؟£¬ئن¶شس¦µمةèخھF£¬Nµم£¬ازFN½»DCسعM£®
جطہجهرé£؛
(1)µ±FD=AFت±£¬،÷FDMµؤضـ³¤تا¶àةظ?
ہà±بج½¾؟£؛
(2)µ±FD،ظAF،ظ0ت±£¬،÷FDMµؤضـ³¤»ل·¢ةْ±ن»¯آً?اëض¤أ÷ؤمµؤ²آد룮
حطص¹رسةى£؛
(3)ح¬رùشعFD،ظAF،ظ0µؤجُ¼دآ£¬ةèAFخھx£¬±»صغئً²؟·ض(¼´£؛ثؤ±كذخFEGN)µؤأو»خھS£¬تشسأ؛¬xµؤ´ْتت½±يت¾S£¬²¢خت£؛µ±xخھ؛خضµت±£¬S=26?
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعئ½أوؤع£¬¸ّ¶¨²»شعح¬ز»جُض±دكةدµؤµم![]() £¨بçح¼ثùت¾£©£¬µم
£¨بçح¼ثùت¾£©£¬µم![]() µ½µم
µ½µم![]() µؤ¾àہë¾ùµبسع
µؤ¾àہë¾ùµبسع![]() (
(![]() خھ³£ت)£¬µ½µم
خھ³£ت)£¬µ½µم![]() µؤ¾àہëµبسع
µؤ¾àہëµبسع![]() µؤثùسذµم×é³ةح¼ذخ
µؤثùسذµم×é³ةح¼ذخ![]() £¬
£¬![]() µؤئ½·ضدك½»ح¼ذخ
µؤئ½·ضدك½»ح¼ذخ![]() سعµم
سعµم![]() £¬ء¬½س
£¬ء¬½س![]() £®
£®
£¨1£©اَض¤£؛![]() £»
£»
£¨2£©¹µم![]() ×÷
×÷![]() £¬´¹×مخھ
£¬´¹×مخھ![]() £¬×÷
£¬×÷![]() £¬´¹×مخھ
£¬´¹×مخھ![]() £¬رس³¤
£¬رس³¤![]() ½»ح¼ذخ
½»ح¼ذخ![]() سعµم
سعµم![]() £¬ء¬½س
£¬ء¬½س![]() £®بô
£®بô![]() £¬اَض±دك
£¬اَض±دك![]() سëح¼ذخ
سëح¼ذخ![]() µؤ¹«¹²µم¸ِت£®
µؤ¹«¹²µم¸ِت£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³تذ³،½«½ّ»ُ¼غخھ40شھ/¼µؤةجئ·°´60شھ/¼تغ³ِ£¬أ؟ذائع؟ةآô³ِ300¼£®تذ³،µ÷²é·´س³£؛بçµ÷صû¼غ¸ٌ£¬أ؟صا¼غ1شھ/¼£¬أ؟ذائع¸أةجئ·زھةظآô³ِ10¼£®
£¨1£©اëذ´³ِ¸أةج³،أ؟شآآô³ِ¸أةجئ·ثù»ٌµأµؤہûبَy£¨شھ£©سë¸أةجئ·أ؟¼صا¼غx£¨شھ£©¼نµؤ؛¯ت¹طدµت½£»
£¨2£©أ؟شآ¸أةج³،دْتغ¸أضضةجئ·»ٌہûؤـ·ٌ´ïµ½6300شھ£؟اëثµأ÷ہيسة£»
£¨3£©اë·ضخِ²¢»ط´ًأ؟¼تغ¼غشعت²أ´·¶خ§ؤع£¬¸أةج³،»ٌµأµؤشآہûبَ²»µحسع6160شھ£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ؤ³ذ£¼ئ»®ز»´خذش¹؛آٍإإاٍ؛حہ؛اٍ£¬أ؟¸ِہ؛اٍµؤ¼غ¸ٌ±بإإاٍ¹َ30شھ£»¹؛آٍ2¸ِإإاٍ؛ح3¸ِہ؛اٍ¹²ذè340شھ£®
(1)اَأ؟¸ِإإاٍ؛حہ؛اٍµؤ¼غ¸ٌ£؛
(2)بô¸أذ£ز»´خذش¹؛آٍإإاٍ؛حہ؛اٍ¹²60¸ِ£¬×ـ·رسأ²»³¬¹3800شھ£¬از¹؛آٍإإاٍµؤ¸ِتةظسع39¸ِ£®ةèإإاٍµؤ¸ِتخھm£¬×ـ·رسأخھyشھ£®
¢ظاَy¹طسعmµؤ؛¯ت¹طدµت½£¬²¢اَm؟ةب،µؤثùسذضµ£»
¢عشعر§ذ£°´شُرùµؤ·½°¸¹؛آٍت±£¬·رسأ×îµح£؟×îµح·رسأخھ¶àةظ£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ôë½اّؤ³ضذر§µؤ¹ْئى»¤خہ¶سذè´س¼×،¢ززء½¶سضذر،شٌز»¶سةي¸ك±ب½دصûئëµؤ¶سش±µ£بخ»¤ئىتض£¬أ؟¶سضذأ؟¸ِ¶سش±µؤةي¸ك£¨µ¥خ»£؛cm£©بçدآ:
¼×¶س | 178 | 177 | 179 | 179 | 178 | 178 | 177 | 178 | 177 | 179 |
زز¶س£؛

·ضخِت¾ف£؛ء½×éرù±¾ت¾فµؤئ½¾ùت،¢ضذخ»ت،¢ضعت،¢·½²îبçدآ±يثùت¾£؛
صûہي،¢أèتِت¾ف:
ئ½¾ùت | ضذخ»ت | ضعت | ·½²î | |
¼×¶س | 178 | 178 | b | 0.6 |
زز¶س | 178 | a | 178 | c |
£¨1£©±يضذa=______£¬b=______£¬c=______£»
£¨2£©¸ù¾ف±ي¸ٌضذµؤت¾ف£¬ؤمبدخھر،شٌؤؤ¸ِ¶س±ب½د؛أ£؟اëثµأ÷ہيسة£®
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com