
����Ŀ��ij�г���������Ϊ40Ԫ/������Ʒ��60Ԫ/���۳���ÿ���ڿ�����300�����г����鷴ӳ��������۸�ÿ�Ǽ�1Ԫ/����ÿ���ڸ���ƷҪ������10����
��1����д�����̳�ÿ����������Ʒ����õ�����y��Ԫ�������Ʒÿ���Ǽ�x��Ԫ����ĺ�����ϵʽ��
��2��ÿ�¸��̳����۸�����Ʒ�����ܷ�ﵽ6300Ԫ����˵�����ɣ�
��3����������ش�ÿ���ۼ���ʲô��Χ�ڣ����̳���õ���������6160Ԫ��
���𰸡���1��y=10x2+100x+6000����2��ÿ�¸��̳����۸�����Ʒ�������ܴﵽ6300Ԫ�����ɼ���������3��ÿ���ۼ۲�����62Ԫ�Ҳ�����68Ԫʱ�����̳���õ���������6160Ԫ
��������
��1������Ʒÿ���Ǽ�x��Ԫ�������̳�ÿ����������Ʒ����õ�����y��Ԫ����������ɵ�y��x�ĺ�����ϵʽ��
��2�����ܣ��Ѻ�����ϵʽ���䷽����Ϊy=-10(x-5)2+6250���ɵ�y�����ֵΪ6250��
��3����-10x2+100x+6000��6160�����x��ȡֵ��Χ���ɣ�
��1������Ʒÿ���Ǽ�x��Ԫ�������̳�ÿ����������Ʒ����õ�����y��Ԫ�������������
![]()
��y=10x2+100x+6000
�ʴ�Ϊ��y=10x2+100x+6000
��2��ÿ�¸��̳����۸�����Ʒ�������ܴﵽ6300Ԫ��
���ɣ���y=10x2+100x+6000=10(x5)2+6250��
��x=5ʱ��yȡ���ֵΪ6250Ԫ��С��6300Ԫ
��ܴﵽ��
��3����������10x2+100x+60006160��
�����ã�x210x+160��
��(x2)(x8)0��
���![]() ���
���![]() ��
��
��ٵã�2x8��
��ڵã�x2��x8���⣬
�൱�ۼ۲�����62Ԫ�Ҳ�����68Ԫʱ���̳���õ���������6160Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���������ε�������ƽ���߽���һ�㣬������Ϊ�����ε�����(������������Բ��Բ��) . ���ڹ涨������ı��ε�������ƽ���߽���һ�㣬���ǰ�������Ϊ���ı��ε����ġ���
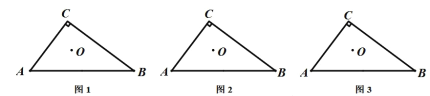
�������
��1����ͼ1������ABC�У���C=90������OΪ��ABC�����ģ���ֱ��DE�ֱ�AC��BC�ڵ�D��E���ҵ�O��ȻΪ�ı���ABED�����ģ�������ֱ��DE���Ի�������?����ͼ1�л���һ������������ֱ��DE������Ҫ˵��������
����̽��
��2����ͼ2������ABC�У���C=90���� AC=3�� BC=4��������(1)��������һ��ֱ��DE // AB�����ʱ�߶�DE�ij���
������
��3����ͼ3������ABC�У���C=90���� AC=3��BC=4�������㣨1�����������߶�DE�Ƿ������Сֵ?������ڣ���������ֵ;��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�羰����Ʊ�۸���ͼ��ʾ���мס������������Ŷӣ��ƻ��ڶ�����ڼ䵽�þ������棬���Ŷ��ο�����֮��Ϊ100�ˣ������Ŷ�����������40�ˣ����Ŷ�����������80�ˣ�����Ŷ�����Ϊ![]() �ˣ�����ס������Ŷӷֱ�����Ʊ�����Ŷ���Ʊ��֮��Ϊ
�ˣ�����ס������Ŷӷֱ�����Ʊ�����Ŷ���Ʊ��֮��Ϊ![]() Ԫ��
Ԫ��

��1��ֱ��д��![]() ����
����![]() �ĺ�����ϵʽ����д���Ա���
�ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2������ס������Ŷ����Ϲ�Ʊ�ȷֱ�Ʊ���ɽ�Լ����Ǯ��
��3���þ���ÿ��11�¡�12��Ϊ������������������������ʵ����Ʊ�����۵��Żݣ������ڼ䲻������Ʊ���������������οͣ���߾������룻�����������з��֣����ŽӴ��ο��������ӣ���������Ӫ�ɱ�Ҳ��֮���ӣ�������Ӫ�ɱ�![]() ����Ԫ�����������ο�������
����Ԫ�����������ο�������![]() �����ˣ�֮�����㺯����ϵʽ��
�����ˣ�֮�����㺯����ϵʽ��![]() ���������ο�������
���������ο�������![]() �����ˣ����㣺
�����ˣ����㣺![]() ���ҵ���ÿ���ο���������ͬ��Ϊ�˻���������������ͨ������ԤԼ��Ʊ�ķ�ʽ���Ƶ���ÿ���ο��������ʾ����ľ����Ƿ���ȷ����˵�����ɣ�������
���ҵ���ÿ���ο���������ͬ��Ϊ�˻���������������ͨ������ԤԼ��Ʊ�ķ�ʽ���Ƶ���ÿ���ο��������ʾ����ľ����Ƿ���ȷ����˵�����ɣ�������![]() ��Ʊ����
��Ʊ����![]() ������Ӫ�ɱ���
������Ӫ�ɱ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������x�ύ��A��B���㣬��y�ύ�ڵ�C��0����2������A�������ǣ�2��0����PΪ�������ϵ�һ�����㣬����P��PD��x���ڵ�D����ֱ��BC�ڵ�E�������ߵĶԳ�����ֱ��x����1��
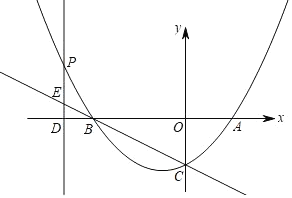
��1���������ߵĺ�������ʽ��
��2������P�ڵڶ������ڣ���PE��![]() OD�����PBE�������
OD�����PBE�������
��3���ڣ�2���������£���MΪֱ��BC��һ�㣬��x����Ϸ����Ƿ���ڵ�M��ʹ��BDM����BDΪ���ĵ��������Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������ͼ��ʾ�Ķ��κ���![]() ��ͼ���У��۲�ó�������������Ϣ����c��0����abc��0����a-b+c��0����
��ͼ���У��۲�ó�������������Ϣ����c��0����abc��0����a-b+c��0����![]() ��4ac����2a=��2b��������ȷ�����ǣ���������
��4ac����2a=��2b��������ȷ�����ǣ���������
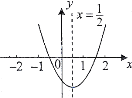
A.�٢ڢ�B.�ڢۢ�C.�ۢܢ�D.�٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ����
����![]() Ϊֱ������Բ��Բ��Ϊ��
Ϊֱ������Բ��Բ��Ϊ��![]() ���Ե�
���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��
Ϊ�뾶��![]() ������
������![]() ��
��![]() ��ƽ���߽������ڵ�
��ƽ���߽������ڵ�![]() ��
��![]() ����ͼ����Ӱ���ֵ�����ǣ� ��
����ͼ����Ӱ���ֵ�����ǣ� ��
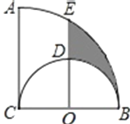
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OΪԭ���ֱ������ϵ�У���A��C�ֱ���x�ᡢy����������ϣ���B�ڵ�һ�����ڣ��ı���OABC�Ǿ��Σ�����������y��![]() ��x��0����AB�ཻ�ڵ�D����BC�ཻ�ڵ�E����BE��4CE���ı���ODBE�������8����k��_____��
��x��0����AB�ཻ�ڵ�D����BC�ཻ�ڵ�E����BE��4CE���ı���ODBE�������8����k��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() �����ڴ˺�����ͼ�����ʣ����н����в�һ����������( )
�����ڴ˺�����ͼ�����ʣ����н����в�һ����������( )
A.��ͼ��Ķ�������Ϊ![]() B.��ͼ����
B.��ͼ����![]() ��Ľ���Ϊ
��Ľ���Ϊ![]()
C.����ͼ����![]() ����һ��������
����һ��������![]() D.��
D.��![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������������£�ij����ר������ij��Ʒ�Ƶ�������Ͳ���ɱ�Ϊ30Ԫ/����ÿ��������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮�����һ�κ�����ϵ����ͼ��ʾ.
��Ԫ��֮�����һ�κ�����ϵ����ͼ��ʾ.

��1����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2������涨ÿ��������Ͳ��������������240���������۵���Ϊ����Ԫʱ��ÿ���ȡ�����������������Ƕ��٣�
��3��������������Ĺ�����ҵ��������ÿ������������о��150Ԫ��ϣ�����̣�Ϊ�˱�֤����ÿ��ʣ��������3600Ԫ����ȷ����������Ͳ���۵��۵ķ�Χ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com