
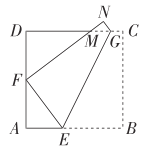
【题目】如图,在正方形ABCD中,DC=8,现将四边形BEGC沿折痕EG(G,E分别在DC,AB边上)折叠,其顶点B,C分别落在边AD上和边DC的上部,其对应点设为F,N点,且FN交DC于M.
特例体验:
(1)当FD=AF时,△FDM的周长是多少?
类比探究:
(2)当FD≠AF≠0时,△FDM的周长会发生变化吗?请证明你的猜想.
拓展延伸:
(3)同样在FD≠AF≠0的条件下,设AF为x,被折起部分(即:四边形FEGN)的面积为S,试用含x的代数式表示S,并问:当x为何值时,S=26?
【答案】(1)16;(2)不变,证明见解析;(3)![]() 当x=2或6时,四边形FEGN的面积为26.
当x=2或6时,四边形FEGN的面积为26.
【解析】
(1)如图1中,在△AEF中,设AE=x,则EF=8-x,AF=4,∠A=90°,理由勾股定理构建方程求出x,再根据△AEF∽△DFM,可得![]() ,由此即可解决问题;
,由此即可解决问题;
(2)△FDM的周长与(1)中结论相同.证明方法与(1)类似;
(3)作GK⊥AB于K.连接BF交GE于P.由△AFB≌△KEG,可得FB=GE,由(2)可知:AE=![]() ,设AF=EK=x,AK=AE+EK=AF+AE=
,设AF=EK=x,AK=AE+EK=AF+AE=![]() ,根据S=
,根据S=![]() ,构建二次函数即可解决问题;
,构建二次函数即可解决问题;
解:(1)在△AEF中,设AE=x,则EF=8-x,AF=4,∠A=90°,
由勾股定理,得:42﹢x2=(8-x)2,
∴x=3,
∴AE=3,EF=5.
∴△AEF的周长为12,
如图,
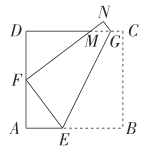
∵∠MFE=90°,
∴∠DFM+∠AFE=90°
又∵∠A=∠D=90,∠AFE=∠DMF,
∴△AEF∽△DFM,
∴![]() =
=![]() =
=![]() ,
,
∴△FDM的周长为16;
(2)△FDM的周长不会发生变化;
理由:如下图,
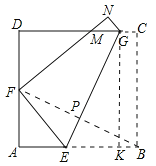
设AF=x,EF=8-AE,x2+AE2=(8-AE)2,
∴AE=![]() ,
,
∵△AEF∽△DFM,
∴![]() ,
,
∴△FMD的周长: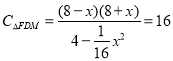 .
.
(3)如图,作GK⊥AB于K.连接BF交GE于P.

∵B、F关于GE对称,
∴BF⊥EG,
∴∠FBE=∠KGE,
在正方形ABCD中,GK=BC=AB,∠A=∠EKG=90°,
∴△AFB≌△KEG,
∴FB=GE,
由(2)可知:AE=![]() ,
,
∴AF=EK=x,AK=AE+EK=AF+AE=![]() ,
,
∴梯形AEGD的面积为:![]() ,
,
∴![]() ,
,
当S=26时,有
![]() ,
,
解得:x=2或x=6,
∴当x=2或6时,四边形FEGN的面积为26.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
①a+b+c<0;②a﹣b+c>1;③abc>0;④9a﹣3b+c<0;⑤c﹣a>1.其中所有正确结论的序号是( )
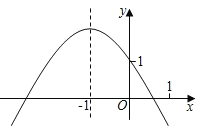
A.①②B.①③④C.①②③④D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(1)第1个等式:a1=![]() ; 第2个等式:a2=
; 第2个等式:a2=![]() ;
;
第3个等式:a3=![]() ; 第4个等式:a4=
; 第4个等式:a4=![]() ;
;
…
用含有n的代数式表示第n个等式:an=___________=___________(n为正整数);
(2)按一定规律排列的一列数依次为![]() ,1,
,1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,按此规律,这列数中的第100个数是_______________.
,…,按此规律,这列数中的第100个数是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,若乙团队人数不超过40人,甲团队人数不超过80人,设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.

(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)该景区每年11月、12月为淡季,景区决定在这两个月实行门票打五折的优惠(打折期间不售团体票),以吸引大量游客,提高景区收入;景区经过调研发现,随着接待游客数的增加,景区的运营成本也随之增加,景区运营成本![]() (万元)与两个月游客总人数
(万元)与两个月游客总人数![]() (万人)之间满足函数关系式:
(万人)之间满足函数关系式:![]() ;两个月游客总人数
;两个月游客总人数![]() (万人)满足:
(万人)满足:![]() ,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润
,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润![]() 门票收入
门票收入![]() 景区运营成本)
景区运营成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.
(1)请用列表或画树状图的方法表示出上述试验所有可能结果;
(2)求一次打开锁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于点C(0,﹣2),点A的坐标是(2,0),P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E,抛物线的对称轴是直线x=﹣1.
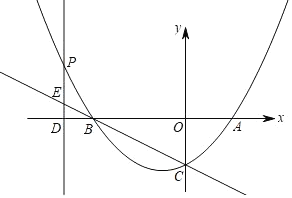
(1)求抛物线的函数表达式;
(2)若点P在第二象限内,且PE=![]() OD,求△PBE的面积.
OD,求△PBE的面积.
(3)在(2)的条件下,若M为直线BC上一点,在x轴的上方,是否存在点M,使△BDM是以BD为腰的等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从如图所示的二次函数![]() 的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④
的图象中,观察得出了下面五条信息:①c>0,②abc<0,③a-b+c>0,④![]() >4ac,⑤2a=-2b,其中正确结论是( ).
>4ac,⑤2a=-2b,其中正确结论是( ).
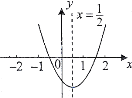
A.①②④B.②③④C.③④⑤D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以O为原点的直角坐标系中,点A,C分别在x轴、y轴的正半轴上,点B在第一象限内,四边形OABC是矩形,反比例函数y=![]() (x>0)与AB相交于点D,与BC相交于点E,若BE=4CE,四边形ODBE的面积是8,则k=_____.
(x>0)与AB相交于点D,与BC相交于点E,若BE=4CE,四边形ODBE的面积是8,则k=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是重庆轻轨10号线龙头寺公园站入口扶梯建设示意图.起初工程师计划修建一段坡度为3:2的扶梯![]() ,扶梯总长为
,扶梯总长为![]() 米.但这样坡度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建
米.但这样坡度大陡,扶梯太长容易引发安全事故.工程师修改方案:修建![]() 、
、![]() 两段扶梯,并减缓各扶梯的坡度,其中扶梯
两段扶梯,并减缓各扶梯的坡度,其中扶梯![]() 和平台
和平台![]() 形成的
形成的![]() 为135°,从
为135°,从![]() 点看
点看![]() 点的仰角为36.5°,
点的仰角为36.5°,![]() 段扶梯长
段扶梯长![]() 米,则
米,则![]() 段扶梯长度约为( )米(参考数据:
段扶梯长度约为( )米(参考数据:![]() ,
,![]() ,
,![]() )
)
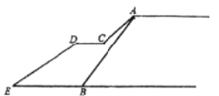
A.43B.45C.47D.49
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com