
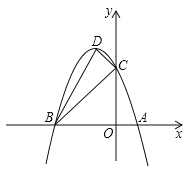
【题目】如图,抛物线与x轴交于A(1,0)、B(-3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)y=-x2-2x+3,(-1,4);(2)△BCD是直角三角形.理由见解析;(3)P1(0,0),P2(0,![]() ),P3(9,0).
),P3(9,0).
【解析】
(1)利用待定系数法即可求得函数的解析式;
(2)利用勾股定理求得△BCD的三边的长,然后根据勾股定理的逆定理即可作出判断;
(3)分p在x轴和y轴两种情况讨论,舍出P的坐标,根据相似三角形的对应边的比相等即可求解.
(1)设抛物线的解析式为y=ax2+bx+c
由抛物线与y轴交于点C(0,3),可知c=3.即抛物线的解析式为y=ax2+bx+3.
把点A(1,0)、点B(-3,0)代入,得![]() 解得a=-1,b=-2
解得a=-1,b=-2
∴抛物线的解析式为y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4
∴顶点D的坐标为(-1,4);
(2)△BCD是直角三角形.
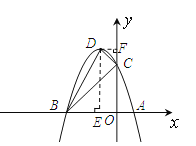
理由如下:过点D分别作x轴、y轴的垂线,垂足分别为E、F.
∵在Rt△BOC中,OB=3,OC=3,
∴BC2=OB2+OC2=18
在Rt△CDF中,DF=1,CF=OF-OC=4-3=1,
∴CD2=DF2+CF2=2
在Rt△BDE中,DE=4,BE=OB-OE=3-1=2,
∴BD2=DE2+BE2=20
∴BC2+CD2=BD2
∴△BCD为直角三角形.
(3)①△BCD的三边,![]() ,又
,又![]() ,故当P是原点O时,△ACP∽△DBC;
,故当P是原点O时,△ACP∽△DBC;
②当AC是直角边时,若AC与CD是对应边,设P的坐标是(0,a),则PC=3-a,![]() ,即
,即![]() ,解得:a=-9,则P的坐标是(0,-9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;
,解得:a=-9,则P的坐标是(0,-9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;
③当AC是直角边,若AC与BC是对应边时,设P的坐标是(0,b),则PC=3-b,则![]() ,即
,即![]() ,解得:b=-
,解得:b=-![]() ,故P是(0,-
,故P是(0,-![]() )时,则△ACP∽△CBD一定成立;
)时,则△ACP∽△CBD一定成立;
④当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(d,0).
则AP=1-d,当AC与CD是对应边时,
![]() ,即
,即![]() ,解得:d=1-3
,解得:d=1-3![]() ,此时,两个三角形不相似;
,此时,两个三角形不相似;
⑤当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(e,0).
则AP=1-e,当AC与DC是对应边时,![]() ,解得:e=-9,符合条件.
,解得:e=-9,符合条件.
总之,符合条件的点P的坐标为:P1(0,0),P2(0,![]() ),P3(9,0).
),P3(9,0).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△DAC=( )

A.1:25B.1:20C.1:18D.1:16
查看答案和解析>>
科目:初中数学 来源: 题型:
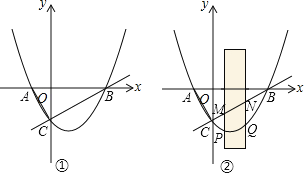
【题目】如图①,直线y=![]() 与x轴、y轴分别交于点B,C,抛物线y=
与x轴、y轴分别交于点B,C,抛物线y=![]() 过B,C两点,且与x轴的另一个交点为点A,连接AC.
过B,C两点,且与x轴的另一个交点为点A,连接AC.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点D(与点A不重合),使得S△DBC=S△ABC,若存在,求出点D的坐标;若不存在,请说明理由;
(3)有宽度为2,长度足够长的矩形(阴影部分)沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线CB于点M和点N,在矩形平移过程中,当以点P,Q,M,N为顶点的四边形是平行四边形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为长春市的一道亮丽的风景线.某社会实践活动小组为了了解“共享单车”的使用情况,对本校师生在7月6日至7月10日使用单车的情况进行了问卷调查. 以下是根据调查结果绘制的统计图的一部分:
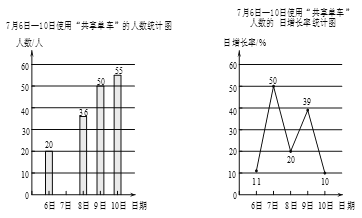
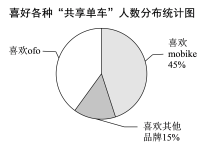
请根据以上信息解答下列问题:
(1)7月7日使用“共享单车”的师生有_________人.
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的师生做了进一步调查,每个人都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢mobike的师生有36人.求喜欢ofo的师生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育文化公司为某学校捐赠甲、乙两种品牌的体育器材,甲品牌有A、B、C三种型号,乙品牌有D、E两种型号,现要从甲、乙两种品牌的器材中各选购一种型号进行捐赠.
(1)下列事件是不可能事件的是 .
A.选购乙品牌的D型号 B.既选购甲品牌也选购乙品牌
C.选购甲品牌的A型号和乙品牌的D型号 D.只选购甲品牌的A型号
(2)写出所有的选购方案(用列表法或树状图);
(3)如果在上述选购方案中,每种方案被选中的可能性相同,那么A型器材被选中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用1200元购进一批甲玩具,用800元购进一批乙玩具,所购甲玩具件数是乙玩具件数的![]() ,已知甲玩具的进货单价比乙玩具的进货单价多1元.
,已知甲玩具的进货单价比乙玩具的进货单价多1元.
(1)求:甲、乙玩具的进货单价各是多少元?
(2)玩具售完后,超市决定再次购进甲、乙玩具(甲、乙玩具的进货单价不变),购进乙玩具的件数比甲玩具件数的2倍多60件,求:该超市用不超过2100元最多可以采购甲玩具多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°得到△EFC,连接AF、BE.
(1)求证:四边形ABEF是平行四边形;
(2)当∠ABC为多少度时,四边形ABEF为矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
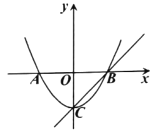
【题目】如图,已知顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,且
两点,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求二次函数![]() 的解析式;
的解析式;
(3)作直线![]() ,问抛物线
,问抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() .若存在,求出点
.若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com