
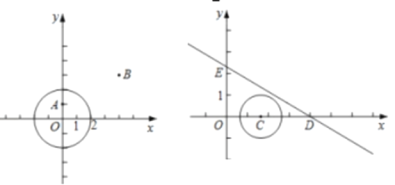
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ёшіцИзПВ¶ЁТеЈәИфөгPФЪНјРОMЙПЈ¬өгQФЪНјРОNЙПЈ¬іЖПЯ¶ОPQіӨ¶ИөДЧоРЎЦөОӘНјРОMЈ¬NөДГЬҫаЈ¬јЗОӘdЈЁMЈ¬NЈ©Ј®МШұрөШЈ¬ИфНјРОMЈ¬NУР№«№ІөгЈ¬№ж¶ЁdЈЁMЈ¬NЈ©=0Ј®
ЈЁ1Ј©ИзНј1Ј¬ЎСOөД°лҫ¶ОӘ2Ј¬
ўЩөгAЈЁ0Ј¬1Ј©Ј¬BЈЁ4Ј¬3Ј©Ј¬ФтdЈЁAЈ¬ЎСOЈ©= Ј¬dЈЁBЈ¬ЎСOЈ©= Ј®
ўЪТСЦӘЦұПЯLЈәy=![]() УлЎСOөДГЬҫаdЈЁLЈ¬ЎСOЈ©=
УлЎСOөДГЬҫаdЈЁLЈ¬ЎСOЈ©=![]() Ј¬ЗуbөДЦөЈ®
Ј¬ЗуbөДЦөЈ®
ЈЁ2Ј©ИзНј2Ј¬CОӘxЦбХэ°лЦбЙПТ»өгЈ¬ЎСCөД°лҫ¶ОӘ1Ј¬ЦұПЯy=©Ғ![]() УлxЦбҪ»УЪөгDЈ¬УлyЦбҪ»УЪөгEЈ¬ЦұПЯDEУлЎСCөДГЬҫаdЈЁDEЈ¬ЎСCЈ©
УлxЦбҪ»УЪөгDЈ¬УлyЦбҪ»УЪөгEЈ¬ЦұПЯDEУлЎСCөДГЬҫаdЈЁDEЈ¬ЎСCЈ©![]()
![]() Ј®ЗлЦұҪУРҙіцФІРДCөДәбЧшұкmөДИЎЦө·¶О§Ј®
Ј®ЗлЦұҪУРҙіцФІРДCөДәбЧшұкmөДИЎЦө·¶О§Ј®
Ўҫҙр°ёЎҝЈЁ1Ј©dЈЁAЈ¬ЎСOЈ©= 1 Ј¬dЈЁBЈ¬ЎСOЈ©= 3 Ј»ЈЁ2Ј©b=![]() Ј»ЈЁ3Ј©
Ј»ЈЁ3Ј©![]() .
.
ЎҫҪвОцЎҝ
ЈЁ1Ј©ўЩБ¬ҪУOB,Ц»РиЗуіцOAЎўOBјҙҝЙҪвҙрЈ»ўЪУГГж»э·ЁЗуіцOKіӨ,ФЩёщҫЭМвТвҪЁБў№ШУЪbөД·ҪіМјҙҝЙҪвҫцОКМвЈ»ЈЁ2Ј©ёщҫЭМвТвЈ¬И·¶ЁCөгФЪxЦбЙПөД·¶О§Ј¬ёщҫЭЗуіцҪзөгЦөАҙИ·¶ЁmөД·¶О§.
ЈЁ1Ј©ўЩИзНјЈ¬Б¬ҪУOBЈ¬№эBөгЧчBHЎНxЦбЈ¬ҙ№ЧгОӘH,
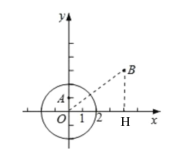
ЎЯЎСOөД°лҫ¶ОӘ2Ј¬өгAЈЁ0Ј¬1Ј©Ј¬
ЎаdЈЁAЈ¬ ЎСOЈ©=2-1=1Ј»
ЎЯB(4Ј¬3)Ј¬ЎаOB=5Ј¬
ЎаdЈЁBЈ¬ЎСOЈ©=5-2=3.
ўЪИзНјЈ¬ЙиЦұПЯУлxЦб,yЦбҪ»PЎўQБҪөгЈ¬№эOЧчOKЎНPQ,ҙ№ЧгОӘK,
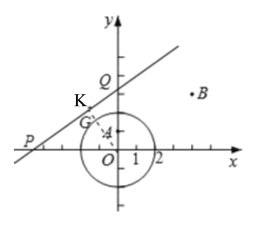
ЎаPЈЁ![]() Ј¬0Ј©ЎўQЈЁ0Ј¬bЈ©Ј¬
Ј¬0Ј©ЎўQЈЁ0Ј¬bЈ©Ј¬
ЎаOP=![]() Ј¬OQ=
Ј¬OQ=![]() Ј¬
Ј¬
УЙ№ҙ№Й¶ЁАнөГЈ¬PQ=![]() Ј¬,
Ј¬,
ЎЯ![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ЎаOK=![]() Ј¬
Ј¬
ЎЯdЈЁLЈ¬ЎСOЈ©=![]() Ј¬
Ј¬
Ўа![]() -2=
-2=![]() Ј¬
Ј¬
Ўаb=ЎА4.
ЈЁ2Ј©ИзНјЈ¬ЧчCRЎНEDУЪөгRЈ¬CSЎНEDУЪөгSЈ¬
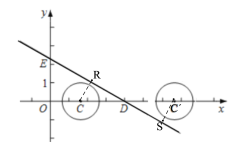
БоCR=CS=![]() Ј¬ФтөгCО»УЪCәНCЦ®јдЈЁ°ьАЁCәНC Ј©Ј¬
Ј¬ФтөгCО»УЪCәНCЦ®јдЈЁ°ьАЁCәНC Ј©Ј¬
ЎЯEЈЁ0Ј¬![]() Ј©Ј¬DЈЁ4Ј¬0Ј©Ј¬
Ј©Ј¬DЈЁ4Ј¬0Ј©Ј¬
ЎаOE=![]() Ј¬OD=4Ј¬УЙ№ҙ№Й¶ЁАнөГЈ¬ED=
Ј¬OD=4Ј¬УЙ№ҙ№Й¶ЁАнөГЈ¬ED=![]() Ј¬
Ј¬
ЎЯsinЎПCDR=![]() Ј¬
Ј¬
Ўа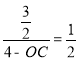 Ј¬
Ј¬
ЎаOC=1Ј¬ЎаOC=7Ј¬
Ўа![]() .
.



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬Т»ЧщөМ°УөДәб¶ПГжОӘМЭРОЈ¬ADЎОBCЈ¬ABЖВЖВҪЗОӘ45ЎгЈ¬DCЖВЖВ¶ИОӘ1Јә2Ј¬ЖдЛыКэҫЭИзНјЛщКҫЈ¬ЗуBCөДіӨЈ®ЈЁҪб№ыұЈБфёщәЕЈ©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
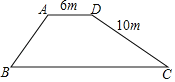
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘABКЗЎСPөДЦұҫ¶Ј¬өг![]() ФЪЎСPЙПЈ¬
ФЪЎСPЙПЈ¬![]() ОӘЎСPНвТ»өгЈ¬ЗТЎПADCЈҪ90ЎгЈ¬ЦұПЯ
ОӘЎСPНвТ»өгЈ¬ЗТЎПADCЈҪ90ЎгЈ¬ЦұПЯ![]() ОӘЎСPөДЗРПЯЈ®
ОӘЎСPөДЗРПЯЈ®
ўЕ КФЛөГчЈә2ЎПBЈ«ЎПDABЈҪ180Ўг
ўЖ ИфЎПBЈҪ30ЎгЈ¬ADЈҪ2Ј¬ЗуЎСPөД°лҫ¶Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
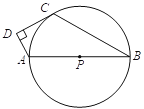
ЎҫМвДҝЎҝИзНјўЩЈ¬BЈ¬CЈ¬EКЗН¬Т»ЦұПЯЙПөДИэёцөгЈ¬ ЛДұЯРОABCDУлЛДұЯРОCEFG¶јКЗХэ·ҪРОЈ®Б¬ҪУBGЈ¬DE.
(1)МҪҫҝBGУлDEЦ®јдөДКэБҝ№ШПөЈ¬ ІўЦӨГчДгөДҪбВЫЈ»
(2)өұХэ·ҪРОCEFGИЖөгCФЪЖҪГжДЪЛіКұХлЧӘ¶ҜөҪИзНјўЪЛщКҫөДО»ЦГКұЈ¬ПЯ¶ОBGәНEDУРәО№ШПө? РҙіцҪбВЫІўЦӨГч.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈҫЕДкј¶(1)°аІҝ·ЦС§ЙъҪУКЬТ»ҙОДЪИЭОӘЎ°ЧоККәПЧФјәөДҝјЗ°јхС№·ҪКҪЎұөДөчІй»о¶ҜЈ¬КХјҜХыАнКэҫЭәуЈ¬АПКҰҪ«јхС№·ҪКҪ·ЦОӘОеАаЈ¬Іў»жЦЖБЛИзНјўЩўЪБҪ·щІ»НкХыөДНіјЖНјЈ¬ЗлёщҫЭНјЦРөДРЕПўҪвҙрПВБРОКМвЈ®
(1)ҫЕДкј¶(1)°аҪУКЬөчІйөДС§Йъ№ІУР¶аЙЩГыЈҝ
(2)І№И«МхРОНіјЖНјЈ¬ІўјЖЛгЙИРОНіјЖНјЦРөДЎ°МеУэ»о¶ҜCЎұЛщ¶ФУҰөДФІРДҪЗ¶ИКэЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНј1Ј¬ҫШРО![]() өД¶Ҙөг
өД¶Ҙөг![]() Ј¬
Ј¬![]() өДЧшұк·ЦұрОӘЈЁ2Ј¬0Ј©Ј¬ЈЁ0Ј¬3Ј© Ј¬ЕЧОпПЯ
өДЧшұк·ЦұрОӘЈЁ2Ј¬0Ј©Ј¬ЈЁ0Ј¬3Ј© Ј¬ЕЧОпПЯ![]() Јә
Јә![]() ҫӯ№э
ҫӯ№э![]() Ј¬
Ј¬![]() БҪөг.ЕЧОпПЯөД¶ҘөгОӘ
БҪөг.ЕЧОпПЯөД¶ҘөгОӘ![]() .
.

ЈЁ1Ј©ЗуЕЧОпПЯ![]() өДұнҙпКҪәНөг
өДұнҙпКҪәНөг![]() өДЧшұкЈ»
өДЧшұкЈ»
ЈЁ2Ј©өг![]() КЗЕЧОпПЯ
КЗЕЧОпПЯ![]() ¶ФіЖЦбЙПТ»¶ҜөгЈ¬өұ
¶ФіЖЦбЙПТ»¶ҜөгЈ¬өұ![]() ОӘөИСьИэҪЗРОКұЈ¬ЗуЛщУР·ыәПМхјюөДөг
ОӘөИСьИэҪЗРОКұЈ¬ЗуЛщУР·ыәПМхјюөДөг![]() өДЧшұкЈ»
өДЧшұкЈ»
ЈЁ3Ј©ИзНј2Ј¬ПЦҪ«ЕЧОпПЯ![]() ҪшРРЖҪТЖЈ¬ұЈіЦ¶ҘөгФЪЦұПЯ
ҪшРРЖҪТЖЈ¬ұЈіЦ¶ҘөгФЪЦұПЯ![]() ЙПЈ¬ИфЖҪТЖәуөДЕЧОпПЯУлЙдПЯ
ЙПЈ¬ИфЖҪТЖәуөДЕЧОпПЯУлЙдПЯ![]() Ц»УРТ»ёц№«№Іөг.ЙиЖҪТЖәуЕЧОпПЯөД¶ҘөгәбЧшұкОӘ
Ц»УРТ»ёц№«№Іөг.ЙиЖҪТЖәуЕЧОпПЯөД¶ҘөгәбЧшұкОӘ![]() Ј¬Зу
Ј¬Зу![]() өДЦө»тИЎЦө·¶О§.
өДЦө»тИЎЦө·¶О§.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ¶юҙОәҜКэyЈҪkx2©ҒЈЁk+3Ј©x+3НјПуөД¶ФіЖЦбОӘЈәЦұПЯxЈҪ2Ј®
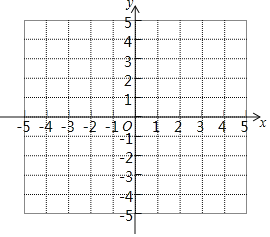
ЈЁ1Ј©ЗуёГ¶юҙОәҜКэөДұнҙпКҪЈ»
ЈЁ2Ј©»ӯіцёГәҜКэөДНјПуЈ¬ІўҪбәПНјПуЦұҪУРҙіцЈә
ўЩөұyЈј0КұЈ¬ЧФұдБҝxөДИЎЦө·¶О§Ј»
ўЪөұ0ЎЬxЈј3КұЈ¬yөДИЎЦө·¶О§КЗ¶аЙЩЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘ¶юҙОәҜКэy=ax2+bx+cөДНјПуУлxЦбПаҪ»УЪAЈЁ©Ғ1Ј¬0Ј©Ј¬BЈЁ3Ј¬0Ј©БҪөгЈ¬УлyЦбПаҪ»УЪөгCЈЁ0Ј¬©Ғ3Ј©Ј®
ЈЁ1Ј©ЗуХвёц¶юҙОәҜКэөДұнҙпКҪЈ»
ЈЁ2Ј©ИфPКЗөЪЛДПуПЮДЪХвёц¶юҙОәҜКэөДНјПуЙПИОТвТ»өгЈ¬PHЎНxЦбУЪөгHЈ¬УлBCҪ»УЪөгMЈ¬Б¬ҪУPCЈ®
ўЩЗуПЯ¶ОPMөДЧоҙуЦөЈ»
ўЪөұЎчPCMКЗТФPMОӘТ»СьөДөИСьИэҪЗРОКұЈ¬ЗуөгPөДЧшұкЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘ![]() Иэёц¶ҘөгөДЧшұк·Цұр
Иэёц¶ҘөгөДЧшұк·Цұр![]() .
.
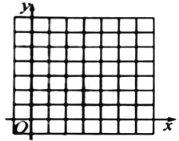
ЈЁ1Ј©»ӯіц![]() Ј»
Ј»
(2)ТФBОӘО»ЛЖЦРРД,Ҫ«![]() ·ЕҙуөҪФӯАҙөД2ұ¶,ФЪУТНјөДНшёсНјЦР»ӯіц·ЕҙуәуөДНјРОЎч
·ЕҙуөҪФӯАҙөД2ұ¶,ФЪУТНјөДНшёсНјЦР»ӯіц·ЕҙуәуөДНјРОЎч![]() Ј»
Ј»
(3)РҙіцөгAөД¶ФУҰөг![]() өДЧшұкЈә___.
өДЧшұкЈә___.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com