
【题目】如图①,B,C,E是同一直线上的三个点, 四边形ABCD与四边形CEFG都是正方形.连接BG,DE.
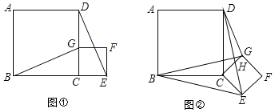
(1)探究BG与DE之间的数量关系, 并证明你的结论;
(2)当正方形CEFG绕点C在平面内顺时针转动到如图②所示的位置时,线段BG和ED有何关系? 写出结论并证明.
【答案】(1)见解析;(2)见解析.
【解析】
(1)猜想BG⊥BD,且BG=DE,延长BG与DE交于H点,用SAS证明△BCG≌△DCE,得出BG=DE,∠CBG=∠CDE,再证明∠DHG=90°,即可得出结论;
(2)用SAS证明△BCG≌△DCE,得出BG=DE,∠CBG=∠CDE,再根据对顶角相等和直角三角形两锐角互余,通过等量代换即可得出结论.
(1)猜想:BG⊥BD,且BG=DE.证明如下:
延长BG与DE交于H点.
∵ABCD和CEFG都是正方形,
∴BC=DC,GC=EC,∠BCG=∠DCE=90°.
在△BCG和△DCE中,∵BC=DC,∠BCG=∠DCE=90°,GC=EC,
∴△BCG≌△DCE,
∴∠BGC=∠DEC,BG=DE.
又∵∠BGC=∠DGH,∠DEC+∠CDE=90°,
∴∠DGH+∠GDH=90°,
∴∠DHG=90°,
故BG⊥DE,且BG=DE.
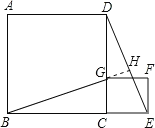
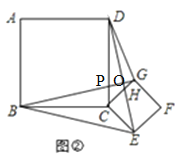
(2)BG=DE,BG⊥DE.证明如下:
∵四边形ABCD、CEFG都是正方形,
∴BC=CD,CG=CE,∠BCD=∠ECG,
∴∠BCG=∠DCE,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE.
又∵∠BPC=∠DPO,∠CBG+∠BPC=90°,
∴∠CDE+∠DPO=90°,
∴∠DOP=90°,
∴BG⊥DE,
∴BG=DE,BG⊥DE.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
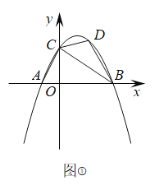
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;
(3)若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k+1)x+4k﹣3=0,
(1)求证:无论k取什么实数值,该方程总有两个不相等的实数根?
(2)当Rt△ABC的斜边a=![]() ,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
,且两条直角边的长b和c恰好是这个方程的两个根时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
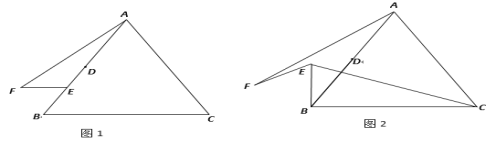
【题目】如图,在边长为8的等边△ABC中,点D是AB的中点,点E是平面上一点,且线段DE=2,将线段EB绕点E顺时针旋转60得到线段EF,连接AF.
(1)如图1,当BE=2时,求线段AF的长;
(2)如图2,求证:AF=CE;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
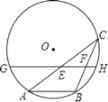
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点.若⊙O的半径为8,则GE+FH的最大值为__________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N上,称线段PQ长度的最小值为图形M,N的密距,记为d(M,N).特别地,若图形M,N有公共点,规定d(M,N)=0.
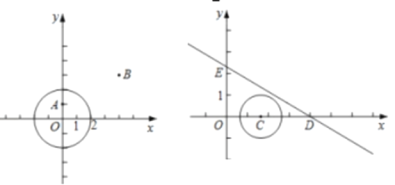
(1)如图1,⊙O的半径为2,
①点A(0,1),B(4,3),则d(A,⊙O)= ,d(B,⊙O)= .
②已知直线L:y=![]() 与⊙O的密距d(L,⊙O)=
与⊙O的密距d(L,⊙O)=![]() ,求b的值.
,求b的值.
(2)如图2,C为x轴正半轴上一点,⊙C的半径为1,直线y=﹣![]() 与x轴交于点D,与y轴交于点E,直线DE与⊙C的密距d(DE,⊙C)
与x轴交于点D,与y轴交于点E,直线DE与⊙C的密距d(DE,⊙C)![]()
![]() .请直接写出圆心C的横坐标m的取值范围.
.请直接写出圆心C的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
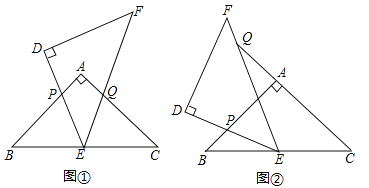
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com