
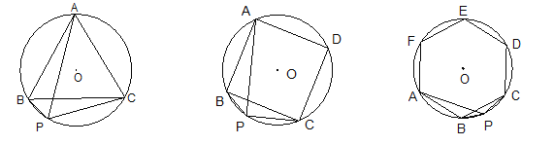
【题目】(1)已知:如图![]() ,
,![]() 是
是![]() 的内接正三角形,点
的内接正三角形,点![]() 为弧
为弧![]() 上一动点,求证:
上一动点,求证:![]() ;
;
(2)如图![]() ,四边形
,四边形![]() 是
是![]() 的内接正方形,点
的内接正方形,点![]() 为弧
为弧![]() 上一动点,求证:
上一动点,求证:![]() ;
;
(3)如图![]() ,六边形
,六边形![]() 是
是![]() 的内接正六边形,点
的内接正六边形,点![]() 为弧
为弧![]() 上一动点,请探究
上一动点,请探究![]() 三者之间有何数量关系,并给予证明.
三者之间有何数量关系,并给予证明.
【答案】(1)答案见解析;(2)答案见解析;(3)![]()
【解析】
(1)延长BP至E,使PE=PC,连接CE,证明△PCE是等边三角形.利用CE=PC,∠E=∠3=60°,∠EBC=∠PAC,得到△BEC≌△APC,所以PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,证明△ABE≌△CBP,所以PC=AE,可得PA=PC+![]() PB.
PB.
(3)在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°,则PQ=![]() PB,PA=PQ+AQ=
PB,PA=PQ+AQ=![]() PB+PC.
PB+PC.
证明:(1)延长BP至E,使PE=PC,
连接CE.∵A、B、P、C四点共圆,

∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.
(2)过点B作BE⊥PB交PA于E.
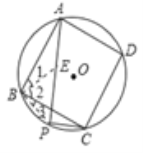
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,∴PE=![]() PB;
PB;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴PA=AE+PE=PC+![]() PB.
PB.
(3)PA=PC+![]() PB,理由如下:
PB,理由如下:
过点B,作BM⊥AP,在AP上截取AQ=PC,连接BQ,
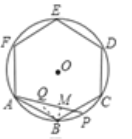
∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=![]() ,
,
∴PM=![]() PB,
PB,
∴PQ=![]() PB
PB
∴PA=PQ+AQ=![]() PB+PC.
PB+PC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
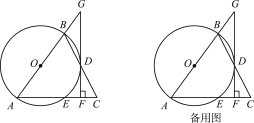
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)求证:DF是⊙O的切线;
(2)已知BD=2![]() ,CF=2,求AE和BG的长.
,CF=2,求AE和BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() -(k+2)x+2k=0.
-(k+2)x+2k=0.
(1)试说明无论k取何值时,这个方程一定有实数根;
(2)已知等腰![]() 的一边a=1,若另两边b、c恰好是这个方程的两个根,求
的一边a=1,若另两边b、c恰好是这个方程的两个根,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字-l,-2和-3.小强从A布袋中随机取出一个小球,记录其标有的数字为a,再从B布袋中随机取出一个小球,记录其标有的数字为b,这样就确定点Q的一个坐标为(a,b).
⑴用列表或画树状图的方法写出点Q的所有可能坐标;
⑵求点Q落在直线y=x-3上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+3经过点A(3,0)和点B(4,3).
(1)求这条抛物线所对应的二次函数的表达式.
(2)直接写出该抛物线开口方向和顶点坐标.
(3)直接在所给坐标平面内画出这条抛物线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化,开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(2)一道数学竞赛题,需要讲16分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y=![]() x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=![]() x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=![]() x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上有一动点P,从O点出发以每秒1个单位的速度沿x轴向右运动,是否存在点P使得△PBC是以P为直角顶点的直角三角形?若存在,求出点P运动的时间t的值,若不存在,请说明理由.
(4)若动点P在x轴上,动点Q在射线AC上,同时从A点出发,点P沿x轴正方向以每秒2个单位的速度运动,点Q以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似,若存在,求a的值,若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com