
【题目】已知关于x的一元二次方程![]() -(k+2)x+2k=0.
-(k+2)x+2k=0.
(1)试说明无论k取何值时,这个方程一定有实数根;
(2)已知等腰![]() 的一边a=1,若另两边b、c恰好是这个方程的两个根,求
的一边a=1,若另两边b、c恰好是这个方程的两个根,求![]() 的周长.
的周长.
【答案】(1)证明详见解析;(2)5.
【解析】
试题用一元二次方程的判别式来判断方程的解的情况,如果判别式大于0,说明一元二次方程有两个不相等的实数根,如果判别式等于0,说明一元二次方程有两个相等的实数根,如果判别式小于0,说明一元二次方程没有实数根.说明此方程有实数根,只要能证明该方程中得△≥0即可求解.
两腰b、c恰好是这个方程的两个根,说明此方程有两个相等的实数根.即△=0.由(1)可知k的取值,然后将k的值代入原方程求根.最后计算△ABC的周长即可.
试题解析:
解:(1)∵![]()
![]()
∴无论取何值时,方程一定有实数根.
由(1)可知:![]() ,即
,即![]()
解得:K=2
当![]() 时,
时,![]()
解得:![]()
即b=c=2
∴△ABC的周长=2+2+1=5


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示A、B、C三点在格点上.

(1)作出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
(2)作出△ABC关于y对称的△A2B2C2,并写出点C2的坐标.
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.

(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
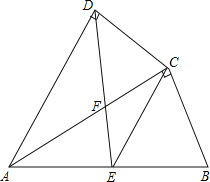
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
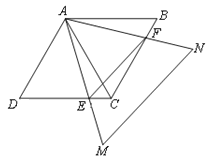
【题目】如图,△ABC、△ADC、△AMN均为等边三角形,AM>AB,AM与DC交于点E,AN与BC交于点F.
(1)试说明:△ABF≌△ACE;
(2)猜测△AEF的形状,并说明你的结论;
(3)请直接指出当F点在BC何处时,AC⊥EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6cm,BC=12cm.. 点M从点A开始沿AB边向点B以1cm/秒的速度向B点移动,点N从点B开始沿BC边以2cm/秒的速度向点C移动. 若M, N分别从A, B点同时出发,设移动时间为t (0<t<6),△DMN的面积为S.
(1) 求S关于t的函数关系式,并求出S的最小值;
(2) 当△DMN为直角三角形时,求△DMN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示,顶点A、F分别在两条平行线上.若A、D、F在一条直线上,则∠1与∠2的数量关系是( )
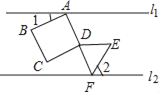
A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2. D. ∠1+2∠2=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com