
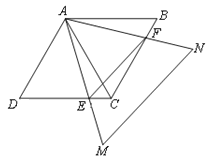
【题目】如图,△ABC、△ADC、△AMN均为等边三角形,AM>AB,AM与DC交于点E,AN与BC交于点F.
(1)试说明:△ABF≌△ACE;
(2)猜测△AEF的形状,并说明你的结论;
(3)请直接指出当F点在BC何处时,AC⊥EF.
【答案】(1)证明见解析;(2)△AEF为等边三角形,证明见解析;(3)当点F为BC中点时,AC⊥EF.
【解析】
(1)由已知条件易得AB=AC,∠B=∠BAC =∠MAN=∠ACD=60°,进而可得∠BAF=∠CAE,由此即可证得△ACE≌△ABF;
(2)由(1)中所得△ACE≌△ABF可得AE=AF,结合∠MAN=60°即可得到△AEF是等边三角形;
(3)当点F为BC中点时,根据“等腰三角形的三线合一”可得∠CAF=∠BAF=30°,结合∠EAF=60°可得∠CAE=∠CAF=30°,结合AE=AF即可得到此时AC⊥EF.
(1)∵△ABC、△ADC均为等边三角形,
∴AB=AC,∠B=∠BAC =∠DAC=∠ACD=60°
∴∠BAC-∠FAC=∠MAN-∠FAC,即∠BAF=∠CAE ,
∴△ACE≌△ABF(AAS);
(2)△AEF为等边三角形,
∵△ACE≌△ABF,
∴AE=AF,
∵△AMN为等边三角形,
∴∠MAN=60°,
∴△AEF为等边三角形;
(3)当点F为BC中点时,AC⊥EF ,理由如下:
∵点F是BC的中点,△ABC是等边三角形,
∴AF平分∠BAC,∠BAC=60°,
∴∠FAC=30°,
又∵△AEF是等边三角形,
∴∠EAF=60°,
∴∠EAC=∠AEF-∠FAC=30°,
∴此时,AC平分∠EAF,
又∵△AEF是等边三角形,
∴AC⊥EF.


科目:初中数学 来源: 题型:
【题目】如图,点B(3,3)在双曲线![]() (x>0)上,点D在双曲线
(x>0)上,点D在双曲线![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(3)求点A的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,A、B两城市相距100km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区.为什么?(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() -(k+2)x+2k=0.
-(k+2)x+2k=0.
(1)试说明无论k取何值时,这个方程一定有实数根;
(2)已知等腰![]() 的一边a=1,若另两边b、c恰好是这个方程的两个根,求
的一边a=1,若另两边b、c恰好是这个方程的两个根,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若四边形ABCD∽四边形A′B′C′D′,AB=6,A′B′=8,∠A=45°,B′C′=8,CD=4,则下列说法错误的是( )
A. ∠A′=45°
B. 四边形A′B′C′D′与四边形ABCD的相似比为![]()
C. BC=6
D. C′D′=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在不等边△ABC中,PM⊥AB,垂足为M,PN⊥AC,垂足为N,且PM=PN,Q在AC上,PQ=QA,下列结论.①AN=AM,②QP∥AM,③△BMP≌△QNP,其中正确的是( )
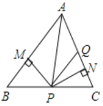
A.①②③B.①②C.②③D.①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在括号内填写理由.
如图所示,已知∠1=∠2,∠B=∠C,可证明AB∥CD,理由如下:

∵∠1=∠2(已知),且∠1=∠4(对顶角相等)
∴∠2=∠4(等量代换)
∴______∥_______(_______)
∴∠______=∠3(________),又∵∠B=∠C(已知),
∴∠3=∠B(等量代换)
∴AB∥CD(__________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com