
【题目】如图.在不等边△ABC中,PM⊥AB,垂足为M,PN⊥AC,垂足为N,且PM=PN,Q在AC上,PQ=QA,下列结论.①AN=AM,②QP∥AM,③△BMP≌△QNP,其中正确的是( )
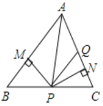
A.①②③B.①②C.②③D.①
【答案】B
【解析】
利用“HL”证明△APM和△APN全等,根据全等三角形对应边相等可得AN=AM;全等三角形对应角相等可得∠PAM=∠PAN,再根据等边对等角可得∠PAN=∠APQ,从而得到∠PAM=∠APQ,然后根据内错角相等,两直线平行可得QP∥AM;欲证△BMP和△QNP全等,须得BP=PQ=AQ,从而得到AC=BC,而此条件无法得到,所以,两三角形不一定全等.
∵PM⊥AB,PN⊥AC,
∴∠AMP=∠ANP=90°,
在Rt△APM和Rt△APN中,![]()
∴Rt△APM≌Rt△APN(HL),
∴AN=AM,故①正确;
∠PAM=∠PAN,
∵PQ=QA,
∴∠PAN=∠APQ,
∴∠PAM=∠APQ,
∴QP∥AM,故②正确;
假设△BMP≌△QNP,
则BP=PQ,
∵PQ=QA,
∴BP=PQ=AQ,
又∵QP∥AM,
∴AC=BC,
此条件无法从题目得到,
所以,假设不成立,故③错误.
综上所述,正确的是①②.
故选B.


科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上,请按要求画图和填空:
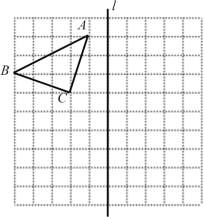
(1)在网格中画出△ABC向下平移5个单位得到的△A1B1C1;
(2)在网格中画出△A1B1C1关于直线l对称的△A2B2C2;
(3)在网格中画出将△ABC绕点A按逆时针方向旋转90度得到的△AB3C3;
(4)在图中探究并求得△ABC的面积= (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
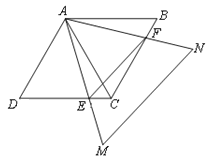
【题目】如图,△ABC、△ADC、△AMN均为等边三角形,AM>AB,AM与DC交于点E,AN与BC交于点F.
(1)试说明:△ABF≌△ACE;
(2)猜测△AEF的形状,并说明你的结论;
(3)请直接指出当F点在BC何处时,AC⊥EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论:①DE=DF,②AE=AF,③BD=CD,④AD⊥BC。其中正确的个数有( )

A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示,顶点A、F分别在两条平行线上.若A、D、F在一条直线上,则∠1与∠2的数量关系是( )
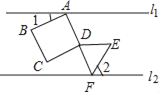
A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2. D. ∠1+2∠2=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC边的垂直平分线DM交AC于D,BC边的垂直平分线EN交BC于E,DM与EN相交于点F.
(1)若△CMN的周长为20cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
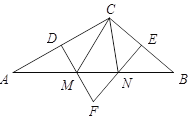
【题目】沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形![]() .
.
(1)图2中的阴影部分的面积为 .
(2)观察图2,请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式.
(3)根据你得到的关系式解答下列问题:若x+y=-6,xy=5,则x–y= .
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的不断发展,越来越多的中学生拥有了自己的手机,某中学课外兴趣小组对使用手机的时间做了调查:随机抽取了该校部分使用手机的中学生进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两种“每周使用手机的时间统计图”(均不完整),请根据统计图表解答以下问题:
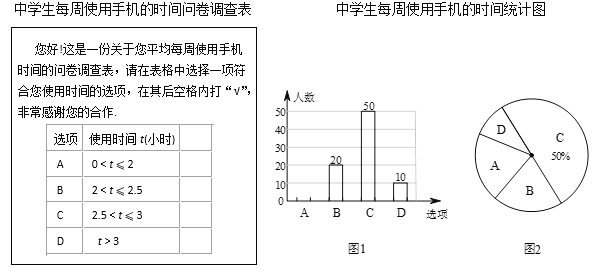
(1)本次接受问卷调查的共有________人;在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名中学生,请你估计该校使用手机的时间在“A”选项的有多少名学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com