
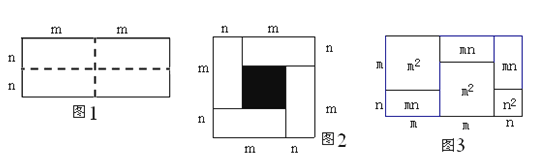
【题目】沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形![]() .
.
(1)图2中的阴影部分的面积为 .
(2)观察图2,请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式.
(3)根据你得到的关系式解答下列问题:若x+y=-6,xy=5,则x–y= .
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
【答案】(1)(mn)2;(2)(m+n)24mn=(mn)2;(3)±4;(4)见解析
【解析】
(1)表示出阴影部分的边长,即可得出其面积;
(2)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式(m+n)2、(mn)2、mn之间的等量关系.
(3)根据(2)所得出的关系式,可求出(xy)2,继而可得出xy的值.
(4)利用已知等式得出符合题意图形即可.
解:(1)图2中的阴影部分的面积为(mn)2;
故填:(mn)2;
(2)代数式(m+n)2、(mn)2、mn之间的等量关系式:(m+n)24mn=(mn)2;
故填:(m+n)24mn=(mn)2;
(3)(xy)2=(x+y)24xy=16,
则xy=±4;
故填:±4;
(4)∵(m+n)(m+3n)=m2+4mn+3n2.
∴如图所示得到图形:


科目:初中数学 来源: 题型:
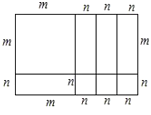
【题目】如图所示,A、B两城市相距100km.现计划在这两座城市间修筑一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上.已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内.请问计划修筑的这条高速公路会不会穿越保护区.为什么?(参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
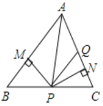
【题目】如图.在不等边△ABC中,PM⊥AB,垂足为M,PN⊥AC,垂足为N,且PM=PN,Q在AC上,PQ=QA,下列结论.①AN=AM,②QP∥AM,③△BMP≌△QNP,其中正确的是( )
A.①②③B.①②C.②③D.①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知□ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD= 2,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形组成的网格中,
的正方形组成的网格中,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() 关于
关于![]() 轴对称的图形为
轴对称的图形为![]() .
.
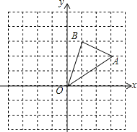
![]() 画出
画出![]() 并写出点
并写出点![]() 的坐标为________;
的坐标为________;
![]() 写出
写出![]() 的面积为________;
的面积为________;
![]() 点
点![]() 在
在![]() 轴上,使
轴上,使![]() 的值最小,写出点
的值最小,写出点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在括号内填写理由.
如图所示,已知∠1=∠2,∠B=∠C,可证明AB∥CD,理由如下:

∵∠1=∠2(已知),且∠1=∠4(对顶角相等)
∴∠2=∠4(等量代换)
∴______∥_______(_______)
∴∠______=∠3(________),又∵∠B=∠C(已知),
∴∠3=∠B(等量代换)
∴AB∥CD(__________)
查看答案和解析>>
科目:初中数学 来源: 题型:
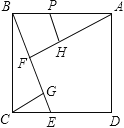
【题目】如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交AB于P.若CG=3.则△CGE与四边形BFHP的面积之和为 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com