
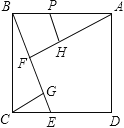
【题目】如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交AB于P.若CG=3.则△CGE与四边形BFHP的面积之和为 _________ .
【答案】9.
【解析】
试题由ABCD为正方形,根据正方形的性质得到AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,又根据CG与BE垂直得到∠BCG+∠CBG=90°,根据同角的余角相等得到一对角相等,又根据一对直角相等,利用“AAS”即可得到三角形BCG与三角形FBA全等,根据全等三角形的对应边相等得到AF与BG相等,又因为FH=FB,从而得到AH=FG,然后由垂直得到一对直角相等,加上一个公共角,得到三角形APH与三角形ABF相似,根据相似得比例,设AH=FG=x,用x表示出PH,由四边形PHFB一组对边平行,另一组对边不平行得到此四边形为梯形,根据梯形的面积公式,由上底PH,下底为BF=3,高FH=3,表示出梯形的面积;然后在三角形BCG与三角形ECG中,根据同角的余角相等,再加上一对直角得到两三角形相似,根据相似得比例,用含x的式子表示出GE,由CG=3,利用表示出的GE,利用三角形的面积公式表示出直角三角形CGE的面积,把表示出的两面积相加,化简即可得到值.
试题解析:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,即∠CBG+∠ABF=90°,
又CG⊥BE,即∠BGC=90°,
∴∠BCG+∠CBG=90°,
∴∠ABF=∠BCG,
又AF⊥BG,
∴∠AFB=∠BGC=90°,
∴△ABF≌△BCG,
∴AF=BG,BF=CG=FH=3,
又∵FH=BF,
∴AH=FG,设AH=FG=x,
∵PH⊥AF,BF⊥AF,
∴∠AHP=∠AFB=90°,又∠PAH为公共角,
∴△APH∽△ABF,
∴![]() ,即PH=
,即PH=![]() ,
,
∵FH∥BF,BP不平行FH,
∴四边形BFHP为梯形,其面积为![]() ;
;
又∵∠BCG+∠ECG=90°,∠ECG+∠BEC=90°,
∴∠BCG=∠BEC,又∠BGC=∠CGE=90°,
∴△BCG∽△CEG,
∴![]() ,即GE=
,即GE=![]() ,
,
故Rt△CGE的面积为![]() ×3×
×3×![]() ,
,
则△CGE与四边形BFHP的面积之和为![]() .
.
考点: 1.正方形的判定与性质;2.全等三角形的判定与性质.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
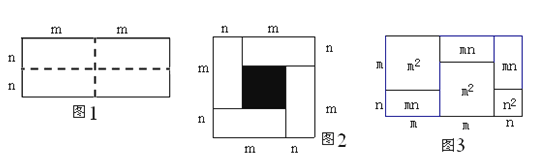
【题目】沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形![]() .
.
(1)图2中的阴影部分的面积为 .
(2)观察图2,请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式.
(3)根据你得到的关系式解答下列问题:若x+y=-6,xy=5,则x–y= .
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(0,3)和点B(﹣2,1)在直线l1:y=kx+b上.
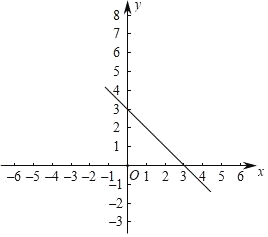
(1)求直线l1的解析式并在平面直角坐标系中画出l1图象;
(2)若直线l1与直线l2:y=﹣x+3交点C,求C点坐标;
(3)请问在y轴上是否存在点P,使得△ACP是等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(0,2),B(4,0),C(4,3)三点.
(1)建立平面直角坐标系并描出A、B、C三点
(2)求△ABC的面积;
(3)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的不断发展,越来越多的中学生拥有了自己的手机,某中学课外兴趣小组对使用手机的时间做了调查:随机抽取了该校部分使用手机的中学生进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两种“每周使用手机的时间统计图”(均不完整),请根据统计图表解答以下问题:
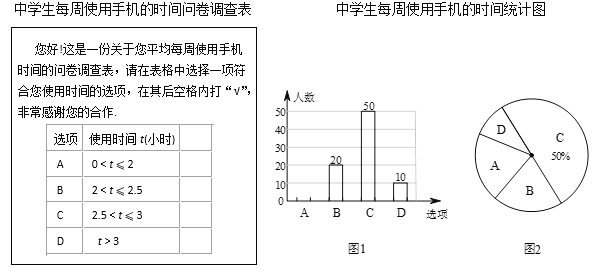
(1)本次接受问卷调查的共有________人;在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名中学生,请你估计该校使用手机的时间在“A”选项的有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,直线AB,CD被直线EF所截,AD是∠CAB的角平分线,若∠3=∠1,∠2=50°,求∠4的度数.

解:∵直线AB与直线EF相交,
∴∠2=∠CAB=50°.( )
∵AD是∠CAB的角平分线,
∴∠1=∠5=![]() ∠CAB=25°,( )
∠CAB=25°,( )
∵∠3=∠1,(已知)
∴∠3=25°,(等量代换)
∴∠3=∠5,(等量代换)
∴_______.( )
∵CD∥AB,( )
∴_______.(两直线平行,同位角相等)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com