
【题目】推理填空:
如图,直线AB,CD被直线EF所截,AD是∠CAB的角平分线,若∠3=∠1,∠2=50°,求∠4的度数.

解:∵直线AB与直线EF相交,
∴∠2=∠CAB=50°.( )
∵AD是∠CAB的角平分线,
∴∠1=∠5=![]() ∠CAB=25°,( )
∠CAB=25°,( )
∵∠3=∠1,(已知)
∴∠3=25°,(等量代换)
∴∠3=∠5,(等量代换)
∴_______.( )
∵CD∥AB,( )
∴_______.(两直线平行,同位角相等)
【答案】对顶角相等;角平分线定义;CD∥AB;内错角相等,两直线平行;已证;∠4=∠2=50°
【解析】
根据平行线的判定及性质求角的过程,一步步把求解的过程补充完整即可.
直线AB与直线EF相交,
∴∠2=∠CAB=50°(对顶角相等),
∵AD是∠CAB的角平分线,
∴∠1=∠DAB=![]() ∠CAB=25°(角平分线的定义),
∠CAB=25°(角平分线的定义),
∵∠3=∠1,(已知)
∴∠3=25°,(等量代换)
∴∠3=∠5,(等量代换)
∴CD∥AB.( 内错角相等,两直线平行)
∵CD∥AB,( 已证)
∴∠4=∠2=50°.(两直线平行,同位角相等)
故答案为:对顶角相等;角平分线定义;CD∥AB,内错角相等,两直线平行;已证;∠4=∠2=50°.


科目:初中数学 来源: 题型:
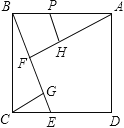
【题目】如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交AB于P.若CG=3.则△CGE与四边形BFHP的面积之和为 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线y=ax2+bx+c过定点M(1,0),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的解析式.小敏写出了一个正确的答案:y=2x2+3x-5.请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c,求该抛物线的顶点最低时的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.

(1)求证:△ABE≌△CDF;
(2)若∠B=60°,AB=4,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC=______°,∠DEC=______°;点D从B向C运动时,∠BDA逐渐变______(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )

A. 10 B. 12 C. 16 D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com