
【题目】如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.

科目:初中数学 来源: 题型:
【题目】随着科技的不断发展,越来越多的中学生拥有了自己的手机,某中学课外兴趣小组对使用手机的时间做了调查:随机抽取了该校部分使用手机的中学生进行调查(问卷调查表如图所示),并用调查结果绘制了图1、图2两种“每周使用手机的时间统计图”(均不完整),请根据统计图表解答以下问题:
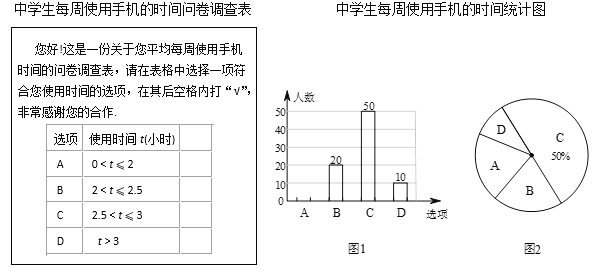
(1)本次接受问卷调查的共有________人;在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名中学生,请你估计该校使用手机的时间在“A”选项的有多少名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国从2008年6月起执行“限塑令”,“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):
65,70,85,75,85,79,74,91,81,95
(1)计算这10名学生所在家庭平均月使用塑料袋多少只?
(2)“限塑令”执行后,家庭平均月使用塑料袋数量预计减少![]() ,根据上面的计算后,你估计该校2000名学生所在的家庭平均月使用塑料袋一共可减少多少只?
,根据上面的计算后,你估计该校2000名学生所在的家庭平均月使用塑料袋一共可减少多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,直线AB,CD被直线EF所截,AD是∠CAB的角平分线,若∠3=∠1,∠2=50°,求∠4的度数.

解:∵直线AB与直线EF相交,
∴∠2=∠CAB=50°.( )
∵AD是∠CAB的角平分线,
∴∠1=∠5=![]() ∠CAB=25°,( )
∠CAB=25°,( )
∵∠3=∠1,(已知)
∴∠3=25°,(等量代换)
∴∠3=∠5,(等量代换)
∴_______.( )
∵CD∥AB,( )
∴_______.(两直线平行,同位角相等)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区中小学开展“阳光体育”大课间活动,某校在大课间中开设了五项活动,A:体操,B:健美操,C:舞蹈,D:球类,E:跑步.为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题:

(1)这次被调查的学生共有 人;
(2)请将统计图1补充完整;
(3)统计图2中D项目对应的扇形的圆心角是 度(保留一位小数);
(4)已知该校共有学生1200人,请根据调查结果估计该校喜欢球类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,

(1)证明:∠APO+∠DCO=30°;
(2)判断△OPC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com