
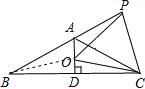
【题目】已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,

(1)证明:∠APO+∠DCO=30°;
(2)判断△OPC的形状,并说明理由.
【答案】(1)见解析;(2)等边三角形,理由见解析
【解析】
(1)利用等边对等角,即可证得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;
(2)证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形.
(1)连接OB.
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°
×120°=60°
∴AD⊥BC,
∴OB=OC,∠ABC=90°﹣∠BAD=30°,
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
(2)等边三角形;
∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°﹣(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形.


科目:初中数学 来源: 题型:
【题目】已知,在四边形ABCD中,∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角,若∠A=α,∠D=β,
(1)如图①,当α+β>180°时,∠F=____(用含α,β的式子表示);
(2)如图②,当α+β<180°时,请在图②中,画出∠F,且∠F=___(用含α,β的式子表示);
(3)当α,β满足条件___时,不存在∠F.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.

(1)求证:△ABE≌△CDF;
(2)若∠B=60°,AB=4,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=_____s时,△POQ是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生综合素养的重要途径,某校为了解学生课外阅读情况,随机抽取若干名学生,调查他们平均每天课外阅读的时间(![]() 小时),并将收集的数据绘制成如图所示的两幅不完整的统计图表,请根据图表信息,解答下列问题:
小时),并将收集的数据绘制成如图所示的两幅不完整的统计图表,请根据图表信息,解答下列问题:
某校学生平均每天课外阅读时间频数表
类别 | 时间 | 频数(人) | 频率 |
A |
| 10 |
|
B |
| 20 | 0.4 |
C |
| 15 | 0.3 |
D |
|
|
|
某校学生平均每天课外阅读时间条形统计图

(1)填空:![]() ________,
________,![]()
![]() ________;并在图中补全条形统计图;
________;并在图中补全条形统计图;
(2)该校现有学生1200人,请你根据上述调查结果,估计该校学生平均每天课外阅读时间不少于1小时的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(1)如图1,在长度为1个单位长度的小正方形组成的正方形中,点A、B、C在小正方形的顶点上.
①在图中画出与△ABC关于直线l成轴对称的△AB′C′;
②在直线l上找一点P,使PB+PC的长最短.

(2)利用网格(图2)作图,请你先在图中的BC边上找一点P,使点P到边AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4,面积为12,腰AB的垂直平分线EF交AB于点E,交AC于点F.若D为BC边的中点,M为线段EF上一个动点,则△BDM的周长的最小值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com