
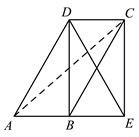
【题目】如图,已知□ABCD,延长AB到E使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=4,CD= 2,求AC的长.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)由已知条件易得四边形BECD是平行四边形及AD=BC,结合ED=AD可得BC=ED,由此可得平行四边形BECD是矩形;
(2)如下图,连接AC,由已知条件和(1)中结论易得BC=AD=4,BE=CD=AB=2,∠AEC=90°,由此在Rt△BCE中,可得CE=![]() ,这样在Rt△ACE中,由勾股定理可得AC=
,这样在Rt△ACE中,由勾股定理可得AC=![]() .
.
(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵BE=AB,
∴BE=CD.
∴四边形BECD是平行四边形.
∵AD=BC,AD =DE,
∴BC=DE.
∴平行四边形BECD是矩形.
(2)如下图,连接AC,
∵AD=4,CD=2,四边形ABCD是平行四边形,四边形BECD是矩形,
∴AB=BE=CD=2,BC=AD=4,∠AEC=90°,
∴AE=AB+BE=4,在Rt△BCE中,CE=![]() ,
,
∴在Rt△ACE中,AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径作半圆⊙O交AC于点D,点E为BC的中点,连接DE.

(1)求证:DE是半圆⊙O的切线;
(2)若∠BAC=30°,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】夹在两条平行线间的正方形ABCD、等边三角形DEF如图所示,顶点A、F分别在两条平行线上.若A、D、F在一条直线上,则∠1与∠2的数量关系是( )
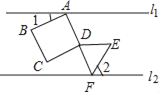
A. ∠1+∠2=60° B. ∠2﹣∠1=30° C. ∠1=2∠2. D. ∠1+2∠2=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC边的垂直平分线DM交AC于D,BC边的垂直平分线EN交BC于E,DM与EN相交于点F.
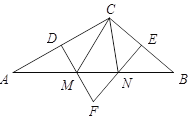
(1)若△CMN的周长为20cm,求AB的长;
(2)若∠MFN=70°,求∠MCN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
![]()
A.小区AB.小区BC.小区CD.AC的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
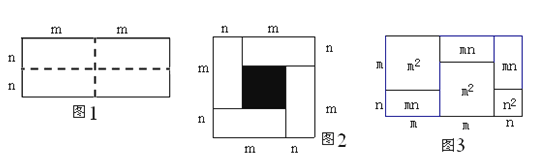
【题目】沿图1长方形中的虚线平均分成四块小长方形,然后按图2的形状拼成一个正方形![]() .
.
(1)图2中的阴影部分的面积为 .
(2)观察图2,请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式.
(3)根据你得到的关系式解答下列问题:若x+y=-6,xy=5,则x–y= .
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2.试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,BE.请根据上述条件,写出一个正确结论.”其中四位同学写出的结论如下:
小青:OE=OF;小何:四边形DFBE是正方形;
小夏:S四边形AFED=S四边形FBCE;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是( )

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com