
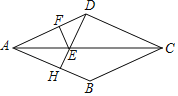
【题目】如图,菱形ABCD中,∠ABC=135°,DH⊥AB于H,交对角线AC于E,过E作EF⊥AD于F.若△DEF的周长为2,则菱形ABCD的面积为( )
A.2![]() B.
B.![]() C.
C.![]() D.2
D.2
【答案】A
【解析】
根据题意利用菱形的性质,可得AH=DH,再根据等腰直角三角形的判定与性质得出DE=![]() EF,再求出DH=DE+EH=
EF,再求出DH=DE+EH=![]() ,利用等腰直角三角形的性质最后得出AB=2.
,利用等腰直角三角形的性质最后得出AB=2.
解:∵四边形ABCD是菱形,∠ABC=135°,
∴∠DAB=45°,∠DAC=∠BAC,且EH⊥AB,EF⊥AD
∴EF=EH,∠ADH=∠DAB=45°
∴AH=DH
∵∠DAB=45°,DH⊥AB
∴∠ADH=45°,且EF⊥AD
∴∠ADH=∠DEF=45°
∴DF=EF,
∴DE=![]() EF
EF
∵△DEF的周长为2,
∴DE+EF+DF=2
∴2EF+![]() EF=2
EF=2
∴EF=2﹣![]()
∴EH=2﹣![]() ,DE=2
,DE=2![]() ﹣2,
﹣2,
∴DH=DE+EH=![]()
∵∠DAB=∠ADH=45°
∴AH=DH=![]() ,
,
∴AD=![]() AH=2
AH=2
∴AB=2
∴菱形ABCD的面积=AB×DH=2![]()
故选:A.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
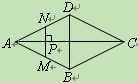
【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查作业:了解你所住小区家庭3月份用气量情况
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2~5之间,这300户家庭的平均人数约为3.3.
小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1抽样调查小区4户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 3 | 4 | 5 |
用气量 | 14 | 19 | 21 | 26 |
表2抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 20 | 22 |
表3抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
根据以|材料回答问题:
(1)小天、小东和小芸三人中,哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处.
(2)在表3中,调查的15个家庭中使用气量的中位数是 m3,众数是 m3.
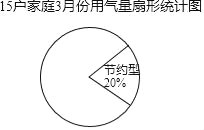
(3)小东将表2中的数据按用气量x(m3)大小分为三类.
①节约型:10≤x≤13,②适中型:14≤x≤17,③偏高型:18≤x≤22,并绘制成如图扇形统讣图,请帮助他将扇形图补充完整.
(4)小芸算出表3中3月份平均每人的用气量为6m3,请估计该小区3月份的总用气量.
查看答案和解析>>
科目:初中数学 来源: 题型:
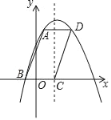
【题目】如图,ABCD与抛物线y=﹣x2+bx+c相交于点A,B,D,点C在抛物线的对称轴上,已知点B(﹣1,0),BC=4.
(1)求抛物线的解析式;
(2)求BD的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,P为BC上的一点,连接AP,过D点作DH⊥AP于H,AB=![]() , BC=4,当△CDH为等腰三角形时,则BP=_________________.
, BC=4,当△CDH为等腰三角形时,则BP=_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里有四张外形相同的卡片卡片上分别标有数字﹣1,1,3,5.摸出一张后,记下数字,再放回,摇匀后再摸出一张,记下数字.以第一次得到的放字为横坐标,第二次得到的数字为纵坐标,得到一个点则这个点.恰好在直线y=﹣x+4上的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解决材料后的问题:
材料一:对于实数x、y,我们将x与y的“友好数”用f(x,y)表示,定义为:f(x)=![]() ,例如17与16的友好数为f(17,16)=
,例如17与16的友好数为f(17,16)=![]() =
=![]() .
.
材料二:对于实数x,用[x]表示不超过实数x的最大整数,即满足条件[x]≤x<[x]+1,例如:
[﹣1.5]=[﹣1.6]=﹣2,[0]=[0.7]=0,[2.2]=[2.7]=2,……
(1)由材料一知:x2+2与1的“友好数”可以用f(x2+2,1)表示,已知f(x2+2,1)=2,请求出x的值;
(2)已知[![]() a﹣1]=﹣3,请求出实数a的取值范围;
a﹣1]=﹣3,请求出实数a的取值范围;
(3)已知实数x、m满足条件x﹣2[x]=![]() ,且m≥2x+
,且m≥2x+![]() ,请求f(x,m2﹣
,请求f(x,m2﹣![]() m)的最小值.
m)的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当y≤![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
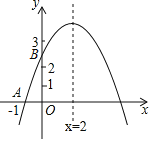
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com