
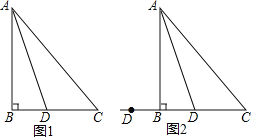
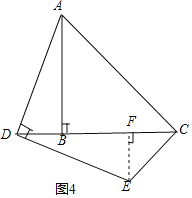
ЁОЬтФПЁПдкЁїABCжаЃЌABЃНBCЃЌЁЯBЃН90ЁуЃЌЕуDЮЊжБЯпBCЩЯЕФвЛИіЖЏЕу(ВЛгыBЁЂCжиКЯ)ЃЌСЌНсADЃЌНЋЯпЖЮADШЦЕуDАДЫГЪБеыЗНЯђа§зЊ90ЁуЃЌЪЙЕуAа§зЊЕНЕуEЃЌСЌНсECЃЎ
(1)ШчЙћЕуDдкЯпЖЮBCЩЯдЫЖЏЃЌШчЭМ1ЃК
ЂйвРЬтвтВЙШЋЭМ1ЃЛ
ЂкЧѓжЄЃКЁЯBADЃНЁЯEDCЃЛ
ЂлЭЈЙ§ЙлВьЁЂЪЕбщЃЌаЁУїЕУГіНсТлЃКдкЕуDдЫЖЏЕФЙ§ГЬжаЃЌзмгаЁЯDCEЃН135ЁуЃЌЃЎ
аЁУїгыЭЌбЇЬжТлКѓЃЌаЮГЩСЫжЄУїетИіНсТлЕФМИжжЯыЗЈЃК
ЯыЗЈвЛЃКдкABЩЯШЁвЛЕуFЃЌЪЙЕУBFЃНBDЃЌвЊжЄЁЯDCEЃН135ЁуЃЌжЛашжЄЁїADFЁеЁїDECЃЎ
ЯыЗЈЖўЃКвдЕуDЮЊдВаФЃЌDCЮЊАыОЖЛЛЁНЛACгкЕуFЃЌвЊжЄЁЯDCEЃН135ЁуЃЌжЛашжЄЁїAFDЁеЁїDCEЃЎ
ЯыЗЈШ§ЃКЙ§ЕуEзїBCЫљдкжБЯпЕФДЙжБЯпЖЮEFЃЌвЊжЄЁЯDCEЃН135ЁуЃЌжЛашжЄEFЃНCFЃЎ
ЧыФуВЮПМЩЯУцЕФЯыЗЈЃЌжЄУїЁЯDCEЃН135Ёу
(2)ШчЙћЕуDдкЯпЖЮCBЕФбгГЄЯпЩЯдЫЖЏЃЌРћгУЭМ2ЛЭМЗжЮіЃЌЁЯDCEЕФЖШЪ§ЛЙЪЧШЗЖЈЕФжЕТ№ЃПШчЙћЪЧЃЌжБНгаДГіЁЯDCEЕФЖШЪ§ЃЛШчЙћВЛЪЧЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)ЂйМћНтЮіЃЛЂкжЄУїМћНтЮіЃЛЂлжЄУїМћНтЮіЃЛ(2)ЁЯDCEЃН45Ёу.
ЁОНтЮіЁП
(1)ЂйИљОнЬтвтзїГіЭМаЮМДПЩЃЛЂкИљОнгрНЧЕФаджЪЕУЕННсТлЃЛЂлжЄЗЈ1ЃКдкABЩЯШЁЕуFЃЌЪЙЕУBFЃНBDЃЌСЌНгDFЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЕУЕНЁЯBFDЃН45ЁуЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНЁЯDCEЃНЁЯAFDЃН135ЁуЃЛжЄЗЈ2ЃКвдDЮЊдВаФЃЌDCЮЊАыОЖзїЛЁНЛACгкЕуFЃЌСЌНгDFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛжЄЗЈ3ЃКЙ§ЕуEзїEFЁЭBCНЛBCЕФбгГЄЯпгкЕуFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛ
(2)Й§EзїEFЁЭDCгкFЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНDBЃНEFЃЌABЃНDFЃНBCЃЌИљОнЯпЖЮЕФКЭВюЕУЕНFCЃНEFЃЌгкЪЧЕУЕННсТлЃЎ
НтЃК(1)ЂйШчЭМЂйЫљЪОЃЛ
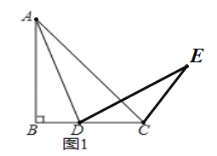
ЂкжЄУїЃКЁпЁЯBЃН90ЁуЃЌ
ЁрЁЯBAD+ЁЯBDAЃН90ЁуЃЌ
ЁпЁЯADEЃН90ЁуЃЌЕуDдкЯпЖЮBCЩЯЃЌ
ЁрЁЯBAD+ЁЯEDCЃН90ЁуЃЌ
ЁрЁЯBADЃНЁЯEDCЃЛ
ЂкжЄЗЈ1ЃКШчЭМЃЌдкABЩЯШЁЕуFЃЌЪЙЕУBFЃНBDЃЌСЌНгDFЃЌ
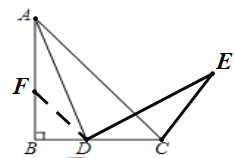
ЁпBFЃНBDЃЌЁЯBЃН90ЁуЃЌ
ЁрЁЯBFDЃН45ЁуЃЌ
ЁрЁЯAFDЃН135ЁуЃЌ
ЁпBAЃНBCЃЌ
ЁрAFЃНCDЃЌ
дкЁїADFКЭЁїDECжаЃЌ
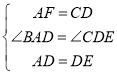
ЁрЁїADFЁеЁїDECЃЌ
ЁрЁЯDCEЃНЁЯAFDЃН135ЁуЃЛ
жЄЗЈ2ЃКвдDЮЊдВаФЃЌDCЮЊАыОЖзїЛЁНЛACгкЕуFЃЌСЌНгDFЃЌ
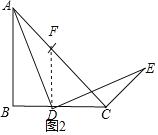
ЁрDCЃНDFЃЌЁЯDFCЃНЁЯDCFЃЌ
ЁпЁЯBЃН90ЁуЃЌABЃНBCЃЌ
ЁрЁЯACBЃН45ЁуЃЌЁЯDFCЃН45ЁуЃЌ
ЁрЁЯDFCЃН90ЁуЃЌЁЯAFDЃН135ЁуЃЌ
ЁпЁЯADEЃНЁЯFDCЃН90ЁуЃЌ
ЁрЁЯADFЃНЁЯEDCЃЌ
дкЁїADFЁеЁїCDEжаЃЌ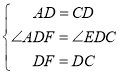 ЃЌ
ЃЌ
ЁрЁїADFЁеЁїCDEЃЌ
ЁрЁЯAFDЃНЁЯDCEЃН135ЁуЃЛ
жЄЗЈ3ЃКЙ§ЕуEзїEFЁЭBCНЛBCЕФбгГЄЯпгкЕуFЃЌ
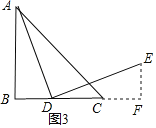
ЁрЁЯEFDЃН90ЁуЃЌ
ЁпЁЯBЃН90ЁуЃЌ
ЁрЁЯEFDЃНЁЯBЃЌ
дкЁїABDКЭЁїDFEжаЃЌ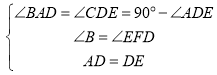 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїDFEЃЌ
ЁрABЃНDFЃЌBDЃНEFЃЌ
ЁпABЃНBCЃЌ
ЁрBCЃНDFЃЌBCЉDCЃНDFЉDCЃЌ
МДBDЃНCFЃЌ
ЁрEFЃНCFЃЌ
ЁпЁЯEFCЃН90ЁуЃЌ
ЁрЁЯECFЃН45ЁуЃЌЁЯDCEЃН135ЁуЃЛ
(2)НтЃКЁЯDCEЃН45ЁуЃЌ
РэгЩЃКЙ§EзїEFЁЭDCгкFЃЌ
ЁпЁЯABDЃН90ЁуЃЌ
ЁрЁЯEDFЃНЁЯDABЃН90ЁуЉЁЯADBЃЌ
дкЁїABDКЭЁїDFEжаЃЌ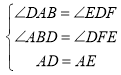 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїDFEЃЌ
ЁрDBЃНEFЃЌABЃНDFЃНBCЃЌ
ЁрBCЉBFЃНDFЉBFЃЌ
МДFCЃНDBЃЌ
ЁрFCЃНEFЃЌ
ЁрЁЯDCEЃН45ЁуЃЎ


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПТЬЩЋГіааЪЧЖдЛЗОГгАЯьзюаЁЕФГіааЗНЪНЃЌЁАЙВЯэЕЅГЕЁБвбГЩЮЊББОЉЕФвЛЕРіІРіЕФЗчОАЯпЃЎФГЩчЛсЪЕМљЛюЖЏаЁ
зщЮЊСЫСЫНтЁАЙВЯэЕЅГЕЁБЕФЪЙгУЧщПіЃЌЖдБОаЃНЬЪІдк3дТ6ШежС3дТ10ШеЪЙгУЕЅГЕЕФЧщПіНјааСЫЮЪОэЕїВщЃЌ
вдЯТЪЧИљОнЕїВщНсЙћЛцжЦЕФЭГМЦЭМЕФвЛВПЗжЃК
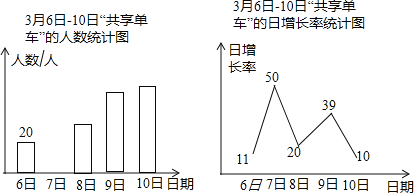
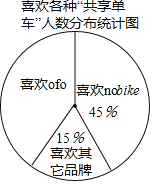
ЧыИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ3дТ7ШеЪЙгУЁАЙВЯэЕЅГЕЁБЕФНЬЪІШЫЪ§ЮЊШЫЃЌВЂЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉВЛЭЌЦЗХЦЕФЁАЙВЯэЕЅГЕЁБИїОпЬиЩЋЃЌЩчЛсЪЕМљЛюЖЏаЁзщеыЖдгаЙ§ЪЙгУЁАЙВЯэЕЅГЕЁБОРњЕФНЬЪІзіСЫНјвЛВНЕїВщЃЌУПЮЛНЬЪІЖМАДвЊЧѓбЁдёСЫвЛжжздМКЯВЛЖЕФЁАЙВЯэЕЅГЕЁБЃЌЭГМЦНсЙћШчЭМЃЌЦфжаЯВЛЖ![]() ЕФНЬЪІга36ШЫЃЌЧѓЯВЛЖ
ЕФНЬЪІга36ШЫЃЌЧѓЯВЛЖ![]() ЕФНЬЪІЕФШЫЪ§ЃЎ
ЕФНЬЪІЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЕФжаЕуЃЌНЋ
ЕФжаЕуЃЌНЋ![]() би
би![]() ЗелЃЌЕУЕН
ЗелЃЌЕУЕН![]() ЃЌ
ЃЌ![]() ЕФбгГЄЯпНЛ
ЕФбгГЄЯпНЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
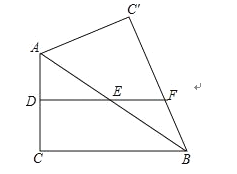
ЃЈ1ЃЉХаЖЯ![]() ЕФаЮзДЮЊ ЃЛ
ЕФаЮзДЮЊ ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓжЄЫФБпаЮ
ЪБЃЌЧѓжЄЫФБпаЮ![]() ЮЊе§ЗНаЮЃЛ
ЮЊе§ЗНаЮЃЛ
ЃЈ3ЃЉШє![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌжБНгаДГі
ЪБЃЌжБНгаДГі![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЮЊФГЧјгђВПЗжНЛЭЈЯпТЗЭМЃЌЦфжажБЯп![]() ЃЌжБЯп
ЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЖМДЙжБЃЌДЙзуЗжБ№Еу
ЖМДЙжБЃЌДЙзуЗжБ№Еу![]() ЁЂЕу
ЁЂЕу![]() КЭЕу
КЭЕу![]() ЃЌЃЈИпЫйТЗгвВрБпдЕЃЉЃЌ
ЃЌЃЈИпЫйТЗгвВрБпдЕЃЉЃЌ![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ЮЛгкЕу
ЮЛгкЕу![]() ЕФББЦЋЖЋ
ЕФББЦЋЖЋ![]() ЗНЯђЩЯЃЌЧв
ЗНЯђЩЯЃЌЧв![]() ЧЇУзЃЌ
ЧЇУзЃЌ![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ЮЛгкЕу
ЮЛгкЕу![]() ЕФББЦЋЖЋ
ЕФББЦЋЖЋ![]() ЗНЯђЩЯЃЌЧв
ЗНЯђЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() ЧЇУзЃЎЕу
ЧЇУзЃЎЕу![]() КЭЕу
КЭЕу![]() ЪЧГЧМЪЯп
ЪЧГЧМЪЯп![]() ЩЯЕФСНИіЯрСкЕФеОЕуЃЎ
ЩЯЕФСНИіЯрСкЕФеОЕуЃЎ
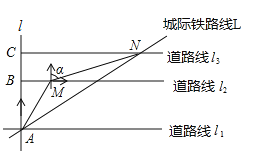
ЃЈ1ЃЉЧѓ![]() КЭ
КЭ![]() жЎМфЕФОрРыЃЛ
жЎМфЕФОрРыЃЛ
ЃЈ2ЃЉШєГЧМЪЛ№ГЕЦНОљЪБЫйЮЊ![]() ЧЇУз/аЁ
МЃЌЧѓЪаУёаЁЧПГЫзјГЧМЪЛ№ГЕДгеОЕу
ЧЇУз/аЁ
МЃЌЧѓЪаУёаЁЧПГЫзјГЧМЪЛ№ГЕДгеОЕу![]() ЕНеОЕу
ЕНеОЕу![]() ашвЊЖрЩйаЁЪБЃПЃЈНсЙћгУЗжЪ§БэЪОЃЉ
ашвЊЖрЩйаЁЪБЃПЃЈНсЙћгУЗжЪ§БэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
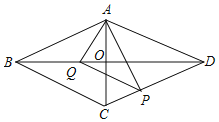
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЕуAЃЌBЃЌCШ§ЕудкЁбOЩЯЃЌAEЦНЗжЁЯBACЃЌНЛЁбOгкЕуEЃЌНЛBCгкЕуDЃЌЙ§ЕуEзїжБЯпlЁЮBCЃЌСЌНсBEЃЎ
(1)ЧѓжЄЃКжБЯпlЪЧЁбOЕФЧаЯпЃЛ
(2)ШчЙћDEЃНaЃЌAEЃНbЃЌаДГіЧѓBEЕФГЄЕФЫМТЗЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
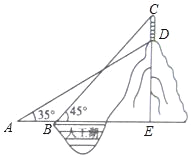
ЁОЬтФПЁПФГЙЋдАЕФШЫЙЄКўБпЩЯгавЛзљМйЩНЃЌМйЩНЖЅЩЯгавЛЪњЦ№ЕФНЈжўЮяCDЃЌИпЮЊ10УзЃЌЪ§бЇаЁзщЮЊСЫВтСПМйЩНЕФИпЖШDEЃЌдкЙЋдАевСЫвЛЫЎЦНЕиУцЃЌдкAДІВтЕУНЈжўЮяЕуDЃЈМДЩНЖЅЃЉЕФбіНЧЮЊ35ЁуЃЌбиЫЎЦНЗНЯђЧАНј20УзЕНДяBЕуЃЌВтЕУНЈжўЮяЖЅВПCЕуЕФбіНЧЮЊ45ЁуЃЌЧѓМйЩНЕФИпЖШDEЃЎЃЈНсЙћОЋШЗЕН1УзЃЌВЮПМЪ§ОнЃКsin35ЁуЁж![]() ЃЌcos35ЁуЁж
ЃЌcos35ЁуЁж![]() ЃЌtan35ЁуЁж
ЃЌtan35ЁуЁж![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСтаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() ЃЌ
ЃЌ![]() ЃЌЖЏЕу
ЃЌЖЏЕу![]() ЁЂ
ЁЂ![]() ЗжБ№ДгЕу
ЗжБ№ДгЕу![]() ЁЂ
ЁЂ![]() ЭЌЪБГіЗЂЃЌдЫЖЏЫйЖШЖМЪЧ
ЭЌЪБГіЗЂЃЌдЫЖЏЫйЖШЖМЪЧ![]() ЃЌЕу
ЃЌЕу![]() гЩ
гЩ![]() Яђ
Яђ![]() дЫЖЏЃЛЕу
дЫЖЏЃЛЕу![]() гЩ
гЩ![]() Яђ
Яђ![]() дЫЖЏЃЌЕБ
дЫЖЏЃЌЕБ![]() ЕНДя
ЕНДя![]() ЪБЃЌ
ЪБЃЌ![]() ЁЂ
ЁЂ![]() СНЕудЫЖЏЭЃжЙЃЌЩшЪБМфЮЊ
СНЕудЫЖЏЭЃжЙЃЌЩшЪБМфЮЊ![]() Уы(
Уы(![]() )ЃЎСЌНг
)ЃЎСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
(1)ЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЃЛ
ЃЛ
(2)Щш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧыаДГі
ЃЌЧыаДГі![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЕФУцЛ§ЪЧЫФБпаЮ
ЕФУцЛ§ЪЧЫФБпаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЃП
ЃП
(4)ЪЧЗёДцдк![]() жЕЃЌЪЙЕУЯпЖЮ
жЕЃЌЪЙЕУЯпЖЮ![]() ОЙ§
ОЙ§![]() ЕФжаЕу
ЕФжаЕу![]() ЃПШєДцдкЃЌЧѓГі
ЃПШєДцдкЃЌЧѓГі![]() жЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
жЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊжБЯпl1ЃКy=mx(mЁй0) гыжБЯпl2ЃКy=ax+b(aЁй0) ЯрНЛгкЕу AЃЈ1ЃЌ2ЃЉЃЌжБЯпl2гы xжсНЛгкЕуBЃЈ3ЃЌ0ЃЉЃЎ
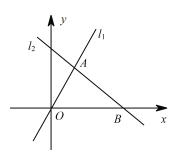
ЃЈ1ЃЉЗжБ№ЧѓжБЯпl1 КЭl2ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЙ§ЖЏЕуPЃЈ0ЃЌnЃЉЧвЦНаагкxжсЕФжБЯпгыl1 ЃЌl2ЕФНЛЕуЗжБ№ЮЊC ЃЌDЃЌЕБЕу C ЮЛгкЕу D зѓЗНЪБЃЌаДГі nЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаетбљвЛИіЮЪЬтЃКЬНОПКЏЪ§![]() ЕФЭМЯѓгыаджЪЃЎ
ЕФЭМЯѓгыаджЪЃЎ
аЁЖЋИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдКЏЪ§![]() ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЕФЭМЯѓгыаджЪНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁЖЋЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃЌВЂНтОіЯрЙиЮЪЬтЃК
ЃЈ1ЃЉКЏЪ§![]() ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЕФздБфСПxЕФШЁжЕЗЖЮЇЪЧ ЃЛ
ЃЈ2ЃЉЯТБэЪЧyгыxЕФМИзщЖдгІжЕЃЌЧѓmЕФжЕЃЛ
x | Ё |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | Ё |
y | Ё |
|
|
|
|
|
|
|
|
|
| m | Ё |
ЃЈ3ЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌУшГіСЫвдЩЯБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЎИљОнУшГіЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ4ЃЉНјвЛВНЬНОПЗЂЯжЃЌИУКЏЪ§ЭМЯѓдкЕкЖўЯѓЯоФкЕФзюЕЭЕуЕФзјБъЪЧ![]() ЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌаДГіИУКЏЪ§ЕФЦфЫќаджЪЃЈвЛЬѕМДПЩЃЉ ЃЎ
ЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌаДГіИУКЏЪ§ЕФЦфЫќаджЪЃЈвЛЬѕМДПЩЃЉ ЃЎ
ЃЈ5ЃЉИљОнКЏЪ§ЭМЯѓЙРЫуЗНГЬ![]() ЕФИљЮЊ ЃЎЃЈОЋШЗЕН0.1ЃЉ
ЕФИљЮЊ ЃЎЃЈОЋШЗЕН0.1ЃЉ
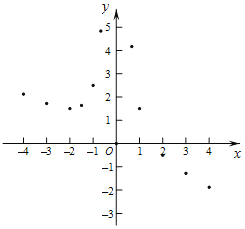
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com