
【题目】如图,点D,E分别在AC,AB上,BD与CE相交于点O,已知∠B=∠C,现添加下面的哪一个条件后,仍不能判定△ABD≌△ACE的是( )

A.AD=AEB.AB=ACC.BD=CED.∠ADB=∠AEC
科目:初中数学 来源: 题型:
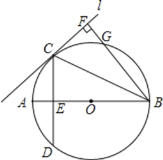
【题目】如图所示,已知AB是![]() 的直径,直线L与
的直径,直线L与![]() 相切于点C,
相切于点C,![]() ,CD交AB于E,
,CD交AB于E,![]() 直线L,垂足为F,BF交
直线L,垂足为F,BF交![]() 于C.
于C.
![]() 图中哪条线段与AE相等?试证明你的结论;
图中哪条线段与AE相等?试证明你的结论;
![]() 若
若![]() ,
,![]() ,求AB的值.
,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
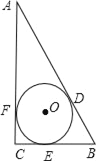
【题目】如图,在Rt△ABC中,∠C=90°,BC=5,⊙O与Rt△ABC的三边AB、BC、AC分别相切于点D、E、F,若⊙O的半径r=2,则Rt△ABC的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
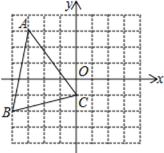
【题目】如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上
(1) 直接写出坐标:A__________,B__________
(2) 画出△ABC关于y轴的对称的△DEC(点D与点A对应)
(3) 用无刻度的直尺,运用全等的知识作出△ABC的高线BF(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列两段材料,再解答下列问题:
(一)例题:分解因式:![]()
解:将“![]() ”看成整体,设
”看成整体,设![]() ,则原式
,则原式![]() ,
,
再将“![]() ”换原,得原式
”换原,得原式![]() ;
;
上述解题目用到的是:整体思想,“整体思想”是数学解题中常用的一种思想方法;
(二)常用因式分解的方法有提公因式法和公式法,但有的多项式只用上述一种方法无法分解,例如![]() ,我们细心观察就会发现,前面两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整分解了.
,我们细心观察就会发现,前面两项可以分解,后两项也可以分解,分别分解后会产生公因式就可以完整分解了.
过程:![]()
![]() ,
,
这种方法叫分组分解法,对于超过三项的多项式往往考虑这种方法.
利用上述数学思想方法解决下列问题:
(1)分解因式:![]()
(2)分解因式:![]()
(3)分解因式:![]() ;
;
查看答案和解析>>
科目:初中数学 来源: 题型:
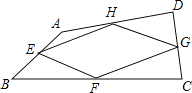
【题目】(满分8分)我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是____________;
(2)证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
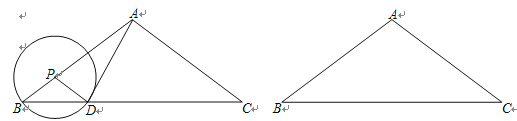
【题目】如图,已知在△ABC中,AB=AC=5,cosB=![]() ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)求△ABC的面积;
(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△APD是直角三角形,求PB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com