
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
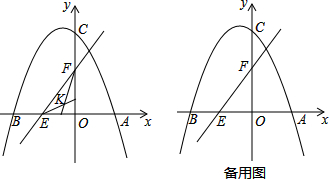
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 各阶梯 | 月用水量 | 基本水价(元、立方米) |
| 第一阶梯 | 不超过28立方米的部分 | 2 |
| 第二阶梯 | 超过28立方米且不超过40立方米的部分 | 2.5 |
| 第三阶梯 | 超过40立方米的部分 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
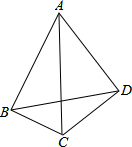 在数学活动中,我们已经学习了四点共圆的条件:如果一个四边形对角互补,那么这个四边形的四个顶点在同一个圆上,简称“四点共圆”.如图,已知四边形ABCD,AD=4,CD=3,AC=5,cos∠BCA=sin∠BAC=$\frac{1}{2}$,求∠BDC的大小.
在数学活动中,我们已经学习了四点共圆的条件:如果一个四边形对角互补,那么这个四边形的四个顶点在同一个圆上,简称“四点共圆”.如图,已知四边形ABCD,AD=4,CD=3,AC=5,cos∠BCA=sin∠BAC=$\frac{1}{2}$,求∠BDC的大小.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
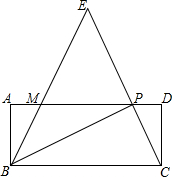 如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP,
如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com