
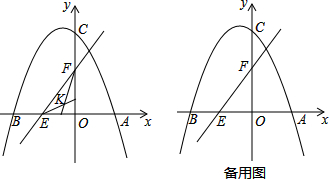
·ÖÎö Łš1Ł©ÀûÓĂŽę¶šÏ”Êę·šÇó”ĂŒŽżÉŁ»
Łš2Ł©žùŸĘÈęœÇĐÎÄÚĐÄ”ÄĐÔÖÊżÉÖȘ$ĄÏKFO=\frac{1}{2}ĄÏEFO$ŁŹĄÏKEO=$\frac{1}{2}$ĄÏFEOŁŹŽÓ¶ű”ĂłöĄÏKFO+ĄÏKEO=$\frac{1}{2}$ŁšĄÏEFO+ĄÏFEOŁ©=$\frac{1}{2}$ĄÁ90Ąă=45ĄăŁź
Łš3Ł©ÏÈÇó”ĂEĄąF”ÄŚű±êŁŹÉèÉäÏßEKœ»yÖáÓÚGŁŹŚśGPĄÍEFÓÚPŁŹÉèOG=xŁŹÔòFG=4-xŁŹPF=EF-EP=EF-EO=5-3=2ŁŹÈ»șóžùŸĘčŽčɶšÀí”Ăłöx2+4=Łš4-xŁ©2ŁŹœâ”ĂOG=$\frac{3}{2}$ŁŹÈ»șó·ÖÁœÖÖÇéżö·Ö±đÌÖÂÛŁŹÍščęÈęœÇĐÎÏàËÆŒŽżÉÇó”Ă”ăD”ÄŚű±êŁ»
Łš4Ł©ÏÈÍščęÁȘÁą·œłÌÇó”ĂĆŚÎïÏßșÍÖ±Ïßœ»”ă”ÄșáŚű±êŁŹÈ»șó·ÖÈęÖÖÇéżö·Ö±đÌÖÂÛŒŽżÉÇó”ĂŁź
œâŽđ 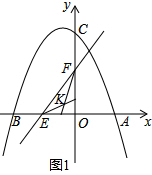 œâŁșŁš1Ł©ÈçÍŒ1ŁŹ°ŃŁš4ŁŹ0Ł©ŁŹŁš-6ŁŹ0Ł©·Ö±đŽúÈëy=-$\frac{1}{3}$x2+bx+cÖĐŁŹ
œâŁșŁš1Ł©ÈçÍŒ1ŁŹ°ŃŁš4ŁŹ0Ł©ŁŹŁš-6ŁŹ0Ł©·Ö±đŽúÈëy=-$\frac{1}{3}$x2+bx+cÖĐŁŹ
Ôò$\left\{\begin{array}{l}{-\frac{1}{3}ĄÁ16+4b+c=0}\\{-\frac{1}{3}ĄÁ36-6b+c=0}\end{array}\right.$
Ąà$\left\{\begin{array}{l}{b=-\frac{2}{3}}\\{c=8}\end{array}\right.$ŁŹ
Ąà¶țŽÎșŻÊę”ÄœâÎöÊœÎȘy=-$\frac{1}{3}$x2-$\frac{2}{3}$x+8Ł»
Łš2Ł©ÈçÍŒ1ŁŹĄßKÊÇĄśEFO”ÄÄÚĐÄŁŹ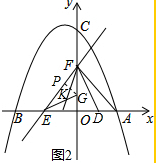
Ąà$ĄÏKFO=\frac{1}{2}ĄÏEFO$ŁŹĄÏKEO=$\frac{1}{2}$ĄÏFEOŁŹ
ĄàĄÏKFO+ĄÏKEO=$\frac{1}{2}$ŁšĄÏEFO+ĄÏFEOŁ©=$\frac{1}{2}$ĄÁ90Ąă=45ĄăŁ»
Łš3Ł©ÓÉÖ±Ïßy=$\frac{4}{3}$x+4żÉÖȘFŁš0ŁŹ4Ł©ŁŹEŁš-3ŁŹ0Ł©ŁŹÈçÍŒ2ŁŹ
ÉèÉäÏßEKœ»yÖáÓÚGŁŹŚśGPĄÍEFÓÚPŁŹ
ÉèOG=xŁŹÔòFG=4-xŁŹPF=EF-EP=EF-EO=5-3=2ŁŹ
Ąàx2+4=Łš4-xŁ©2ŁŹœâ”Ăx=$\frac{3}{2}$ŁŹ
ĄàOG=$\frac{3}{2}$ŁŹ
Èô”ăDÔÚÏ߶ÎOAÉÏŁŹ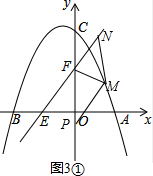
ĄßĄÏDFA+ĄÏDFO=45ĄăŁŹĄÏKFO+ĄÏKEO=45ĄăŁŹĄÏDFA=ĄÏKFOŁŹ
ĄàĄÏDFO=ĄÏGEOŁŹ
ĄàĄśODFĄŚĄśOGEŁŹ
Ąà$\frac{OD}{OF}$=$\frac{OG}{OE}$=$\frac{\frac{3}{2}}{3}$=$\frac{1}{2}$ŁŹ
ĄàOD=2ŁŹ
ĄàDŁš2ŁŹ0Ł©Ł»
Èô”ăDÔÚÏ߶ÎOA”ÄŃÓł€ÏßÉÏŁŹ
ĄßĄÏDFA+ĄÏFDO=45ĄăŁŹĄÏKFO+ĄÏKEO=45ĄăŁŹ
Ó֥ߥÏDFA=ĄÏKFOŁŹ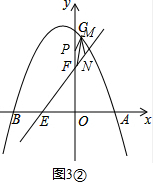
ĄàĄÏFDO=ĄÏGEOŁŹ
ĄàĄśODFĄŚĄśOGEŁŹ
Ąà$\frac{OF}{OD}$=$\frac{OG}{OE}$=$\frac{1}{2}$ŁŹ
ĄàOD=8ŁŹ
ĄàDŁš8ŁŹ0Ł©Ł»
Łš4Ł©MŁš1ŁŹ7Ł©»òŁš3ŁŹ3Ł©»òŁš-4ŁŹ$\frac{16}{3}$Ł©ŁŹ
œâ$\left\{\begin{array}{l}{y=-\frac{1}{3}{x}^{2}-\frac{2}{3}x+8}\\{y=\frac{4}{3}x+4}\end{array}\right.$”Ăx=-3ĄÀ$\sqrt{21}$ŁŹ
ĄàĆŚÎïÏßÓëÖ±Ïßœâ”Ă”ÄșáŚű±êÎȘx1=-3+$\sqrt{21}$ŁŹx2=-3-$\sqrt{21}$ŁŹ
ÉèMŁšxŁŹ-$\frac{1}{3}$x2-$\frac{2}{3}$x+8Ł©ŁŹNŁšxŁŹ$\frac{4}{3}$x+4Ł©ŁŹ
ÓÉÌâÒâ”ĂŁșFN=MNŁŹ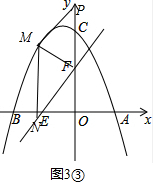
Èô-3+$\sqrt{21}$ŁŒxŁŒ4ŁŹÈçÍŒ3ąÙŁŹÔòMN=$\frac{1}{3}$x2+2x-4ŁŹFN=$\frac{5}{3}$xŁŹ
Ąà$\frac{1}{3}$x2+2x-4=$\frac{5}{3}$xŁŹ
Ąàx1=-4ŁšÉáÈ„Ł©ŁŹx2=3ŁŹ
ĄàMŁš3ŁŹ3Ł©Ł»
Èô0ŁŒxŁŒ-3+$\sqrt{21}$ŁŹÈçÍŒ3ąÚŁŹÔòMN=-$\frac{1}{3}$x2-2x+4ŁŹFN=$\frac{5}{3}$xŁŹ
Ąà-$\frac{1}{3}$x2-2x+4=$\frac{5}{3}$xŁŹ
Ąàx1=-12ŁšÉáÈ„Ł©ŁŹx2=1ŁŹ
ĄàMŁš1ŁŹ7Ł©Ł»
Èô-6ŁŒxŁŒ0ŁŹÈçÍŒ3ąÛŁŹÔòMN=-$\frac{1}{3}$x2-2x+4ŁŹFN=-$\frac{5}{3}$xŁŹ
Ąà-$\frac{1}{3}$x2-2x+4=-$\frac{5}{3}$xŁŹ
Ąàx1=3ŁšÉáÈ„Ł©ŁŹx2=-4ŁŹ
ĄàMŁš-4ŁŹ$\frac{16}{3}$Ł©ŁŹ
ŚÛÉÏM”ă”ÄŚű±êÎȘŁš1ŁŹ7Ł©»òŁš3ŁŹ3Ł©»òŁš-4ŁŹ$\frac{16}{3}$Ł©Łź
”ăÆÀ ±ŸÌâÊǶțŽÎșŻÊę”ÄŚÛșÏÌ⣏żŒČéÁËŽę¶šÏ”Êę·šÇó¶țŽÎșŻÊę”ÄœâÎöÊœŁŹÈęœÇĐΔÄÄÚĐÄŁŹčŽčɶšÀí”ÄÓŠÓĂŁŹÈęœÇĐÎÏàËÆ”ÄĆжšșÍĐÔÖÊŁŹÊęĐÎœáșÏËŒÏë”ÄÔËÓĂÊÇœâÌâ”ÄčŰŒüŁź


 ÓĆÉúÀÖÔ°Ï”ÁĐŽđ°ž
ÓĆÉúÀÖÔ°Ï”ÁĐŽđ°ž бàХѧ”„ÔȘŚÔČâÌâÏ”ÁĐŽđ°ž
бàХѧ”„ÔȘŚÔČâÌâÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
| AŁź | -Łš-3Ł© | BŁź | -|-3| | CŁź | 3-2 | DŁź | Łš-3Ł©2 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșœâŽđÌâ
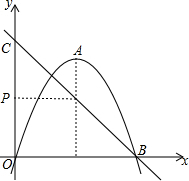 ÈçÍŒŁŹĆŚÎïÏßy=-Łšx+mŁ©2+k”Ķ„”ăA”ÄŚű±êÎȘŁš2ŁŹ4Ł©ŁŹÓëxÖá”ÄŐę°ëÖ᜻ÓÚ”ăBŁŹ”ăC”ÄŚű±êÎȘŁš0ŁŹ4Ł©ŁŹ”ăAŁŹPčŰÓÚÖ±ÏßBC¶ÔłÆŁź
ÈçÍŒŁŹĆŚÎïÏßy=-Łšx+mŁ©2+k”Ķ„”ăA”ÄŚű±êÎȘŁš2ŁŹ4Ł©ŁŹÓëxÖá”ÄŐę°ëÖ᜻ÓÚ”ăBŁŹ”ăC”ÄŚű±êÎȘŁš0ŁŹ4Ł©ŁŹ”ăAŁŹPčŰÓÚÖ±ÏßBC¶ÔłÆŁźČ鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
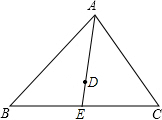 ÈçÍŒŁŹĄśABCÖĐŁŹDÊÇĄśABC”ÄÖŰĐÄŁŹÁŹœÓADČąŃÓł€ŁŹœ»BCÓÚ”ăEŁŹÈôBC=6ŁŹÔòEC=ŁšĄĄĄĄŁ©
ÈçÍŒŁŹĄśABCÖĐŁŹDÊÇĄśABC”ÄÖŰĐÄŁŹÁŹœÓADČąŃÓł€ŁŹœ»BCÓÚ”ăEŁŹÈôBC=6ŁŹÔòEC=ŁšĄĄĄĄŁ©| AŁź | 2 | BŁź | 2.5 | CŁź | 3 | DŁź | 3.5 |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșÌîżŐÌâ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
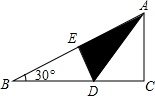 ÈçÍŒŐÛ”țÖ±œÇÈęœÇĐÎÖœÆŹ”ÄÖ±œÇŁŹÊč”ăCÂäÔÚб±ßABÉϔĔăEŽŠŁŹÒŃÖȘCD=1ŁŹĄÏB=30ĄăŁŹÔòBD”Äł€ÊÇŁšĄĄĄĄŁ©
ÈçÍŒŐÛ”țÖ±œÇÈęœÇĐÎÖœÆŹ”ÄÖ±œÇŁŹÊč”ăCÂäÔÚб±ßABÉϔĔăEŽŠŁŹÒŃÖȘCD=1ŁŹĄÏB=30ĄăŁŹÔòBD”Äł€ÊÇŁšĄĄĄĄŁ©| AŁź | 1 | BŁź | 2 | CŁź | $\sqrt{3}$ | DŁź | 2$\sqrt{3}$ |
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁșŃĄÔńÌâ
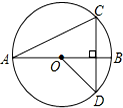 ÈçÍŒŁŹABÊÇĄŃO”ÄÖ±Ÿ¶ŁŹÏÒCDAABŁŹĄÏCAB=20ĄăŁŹÔòĄÏBOD”ÈÓÚŁšĄĄĄĄŁ©
ÈçÍŒŁŹABÊÇĄŃO”ÄÖ±Ÿ¶ŁŹÏÒCDAABŁŹĄÏCAB=20ĄăŁŹÔòĄÏBOD”ÈÓÚŁšĄĄĄĄŁ©| AŁź | 30Ąă | BŁź | 40Ąă | CŁź | 45Ąă | DŁź | 50Ąă |
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com