
已知抛物线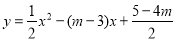 .
.
(1)求证:无论 为任何实数,抛物线与
为任何实数,抛物线与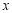 轴总有两个交点;
轴总有两个交点;
(2)若A 、B
、B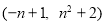 是抛物线上的两个不同点,求抛物线的表达式和
是抛物线上的两个不同点,求抛物线的表达式和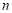 的值;
的值;
(3)若反比例函数 的图象与(2)中的抛物线在第一象限内的交点的横坐标为
的图象与(2)中的抛物线在第一象限内的交点的横坐标为 ,且满足2<
,且满足2< <3,求k的取值范围.
<3,求k的取值范围.
(2)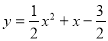 ,
, (3)5<k<18
(3)5<k<18
【解析】
试题分析:(1)根据抛物线的图像与性质可知其与x轴交点的判定条件是 ,因此可由判别式得证结果;
,因此可由判别式得证结果;
(2)根据题意可求得抛物线的对称轴,且有A,B的点可判断它们是对称点,根据对称性可求出m的值,求得抛物线的解析式,然后把A点的坐标代入解析式可求得n的值;
(3)根据二次函数的增减性以及反比例函数的图像与性质,可以判断出两函数之间的大小关系,构成不等式,从而解出k的取值范围.
试题解析:(1)证明:令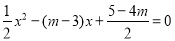 .
.
得

 .
.
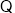 不论m为任何实数,都有(m-1)2+3>0,即△>0.
不论m为任何实数,都有(m-1)2+3>0,即△>0.
∴不论m为任何实数,抛物线与x轴总有两个交点.
 (2)【解析】
(2)【解析】
抛物线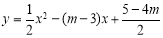 的对称轴为
的对称轴为
∵抛物线上两个不同点A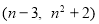 、B
、B 的纵坐标相同,
的纵坐标相同,
∴点A和点B关于抛物线的对称轴对称,则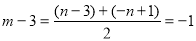 .
.
∴ .
.
∴抛物线的解析式为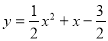 .
.
∵A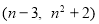 在抛物线
在抛物线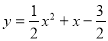 上,
上,
∴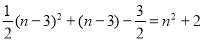 .
.
化简,得 .
.
∴  .
.
(3)当2< <3时,对于
<3时,对于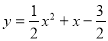 ,y随着x的增大而增大,
,y随着x的增大而增大,
对于 ,y随着x的增大而减小.
,y随着x的增大而减小.
所以当 时,由反比例函数图象在二次函数图象上方,得
时,由反比例函数图象在二次函数图象上方,得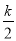 >
> ,
,
解得k>5.
当 时,由二次函数图象在反比例函数图象上方,得
时,由二次函数图象在反比例函数图象上方,得 >
> ,
,
解得k<18.
所以k的取值范围为5<k<18.
考点:二次函数的图像与性质综合题


科目:初中数学 来源:2014-2015学年江苏省太仓市、昆山市七年级上学期期末联考数学试卷(解析版) 题型:选择题
已知太阳的半径约为696000000m,则696000000这个数用科学记数法可表示为 ( ).
A.0.696×109 B.6.96×109
C.6.96×108 D.69.6×107
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省三门峡市九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,正比例函数 与反比例函数
与反比例函数 相交于点E(
相交于点E(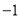 ,2),若
,2),若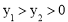 ,则
,则 的取值范围为 .
的取值范围为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市房山区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,做CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,求这个车轮的外圆半径长.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖南省祁阳县九年级下学期期末教学质量检测数学试卷(解析版) 题型:解答题
甲、乙两种水稻试验品种连续5年的平均单位面积产量如下(单位:吨/公顷):
品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
为使水稻品种的产量比较稳定,根据题中所给的数据,你选择哪种水稻品种?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省滨海县七年级上学期期末考试数学试卷(解析版) 题型:选择题
如果∠1与∠2互补,∠2与∠3互余,则∠1与∠3的关系是
A.∠1=∠3 B.∠1=180°-∠3
C.∠1=90°+∠3 D.∠3=90°+∠1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com