Question

【题目】已知正方形ABCD的边长为4，一个以点A为顶点的45°角绕点A旋转，角的两边分别与边BC、DC的延长线交于点E、F，连接EF．设CE=a，CF=b．

（1）如图1，当∠EAF被对角线AC平分时，求a、b的值；
（2）当△AEF是直角三角形时，求a、b的值；
（3）如图3，探索∠EAF绕点A旋转的过程中a、b满足的关系式，并说明理由．

Answer 1

【答案】
（1）

解：∵四边形ABCD是正方形，

∴∠ACF=∠DCD=90°，

∵AC是正方形ABCD的对角线，

∴∠ACB=∠ACD=45°，

∴∠ACF=∠ACE，

∵∠EAF被对角线AC平分，

∴∠CAF=∠CAE，

在△ACF和△ACE中，

，

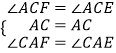∴△ACF≌△ACE，

∴CE=CE，

∵CE=a，CF=b，

∴a=b；

（2）

解：当△AEF是直角三角形时，

①当∠AEF=90°时，

∵∠EAF=45°，

∴∠AFE=45°，

∴△AEF是等腰直角三角形，

∴AF2=2FE2=2（CE2+CF2），

AF2=2（AD2+BE2），

∴2（CE2+CF2）=2（AD2+BE2），

∴CE2+CF2=AD2+BE2，

∴CE2+CF2=16+（4+CE）2，

∴CF2=8（CE+4）①

∵∠AEB+∠BEF=90°，∠AEB+∠BAE=90°，

∴∠BEF=∠BAE，

∴△ABE∽△ECF，

∴ ，

∴ ，

∴4CF=CE（CE+4）②，

联立①②得，CE=4，CF=8

∴a=4，b=8，

②当∠AFE=90°时，

同①的方法得，CF=4，CE=8，

∴a=8，b=4．

（3）

ab=32，

理由：如图，

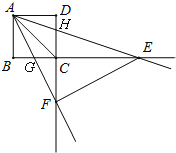
∵∠BAG+∠AGB=90°，∠AFC+∠CGF=90°，∠AGB=∠CGF，

∴∠BAG=∠AFC，

∵∠BAC=45°，

∴∠BAG+∠CAF=45°，

∴∠AFC+∠CAF=45°，

∵∠AFC+∠AEC=180°﹣（∠CFE+∠CEF）﹣∠EAF=180°﹣90°﹣45°=45°，

∴∠CAF=∠AEC，

∵∠ACF=∠ACE=135°，

∴△ACF∽△ECA，

∴ ，

∴EC×CF=AC2=2AB2=32

∴ab=32

【解析】（1）当∠EAF被对角线AC平分时，易证△ACF≌△ACE，因此CF=CE，即a=b．（2）分两种情况进行计算，①先用勾股定理得出CF2=8（CE+4）①，再用相似三角形得出4CF=CE（CE+4）②，两式联立解方程组即可；（3）先判断出∠AFC+∠CAF=45°，再判断出∠AFC+∠AEC=45°，从而求出∠AEC，而∠ACF=∠ACE=135°，得到△ACF∽△ECA，即可．此题是四边形综合题，主要考查了全等三角形的判定和性质，直角三角形的性质，相似三角形的性质和判定，解本题的关键是判断△ACF∽△ECA，也是本题的难点．