
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
【答案】
(1)
解:∵四边形ABCD是正方形,
∴△ABD是等腰直角三角形,
∴2AB2=BD2,
∵BD= ![]() ,
,
∴AB=1,
∴正方形ABCD的边长为1;
(2)
解:CN= ![]() CM.
CM.
证明:∵CF=CA,AF是∠ACF的平分线,
∴CE⊥AF,
∴∠AEN=∠CBN=90°,
∵∠ANE=∠CNB,
∴∠BAF=∠BCN,
在△ABF和△CBN中,
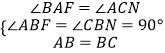 ,
,
∴△ABF≌△CBN(AAS),
∴AF=CN,
∵∠BAF=∠BCN,∠ACN=∠BCN,
∴∠BAF=∠OCM,
∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠ABF=∠COM=90°,
∴△ABF∽△COM,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
即CN= ![]() CM.
CM.
【解析】(1)根据正方形的性质以及勾股定理即可求得;(2)根据等腰三角形三线合一的性质证得CE⊥AF,进一步得出∠BAF=∠BCN,然后通过证得△ABF≌△CBN得出AF=CN,进而证得△ABF∽△COM,根据相似三角形的性质和正方形的性质即可证得CN= ![]() CM.本题考查了正方形的性质,勾股定理的应用,等腰三角形三线合一的性质,三角形全等的判定和性质,三角形相似的判定和性质,熟练掌握性质定理是解题的关键.
CM.本题考查了正方形的性质,勾股定理的应用,等腰三角形三线合一的性质,三角形全等的判定和性质,三角形相似的判定和性质,熟练掌握性质定理是解题的关键.


科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y= ![]() x2﹣
x2﹣ ![]() x+3的绳子.
x+3的绳子. 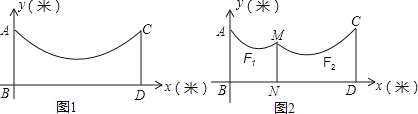
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为 ![]() ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧 ![]() 的长为
的长为 ![]() π,直线y=﹣
π,直线y=﹣ ![]() x+4与x轴、y轴分别交于点A、B.
x+4与x轴、y轴分别交于点A、B. 
(1)求证:直线AB与⊙O相切;
(2)求图中所示的阴影部分的面积(结果用π表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cm
B.18cm
C.20cm
D.21cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.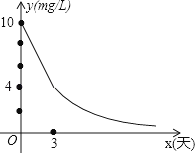
(1)求整改过程中硫化物的浓度y与时间x的函数表达式;
(2)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com