
【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y= ![]() x2﹣
x2﹣ ![]() x+3的绳子.
x+3的绳子. 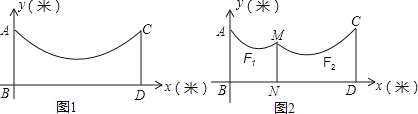
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为 ![]() ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
【答案】
(1)
解:∵a= ![]() >0,
>0,
∴抛物线顶点为最低点,
∵y= ![]() x2﹣
x2﹣ ![]() x+3=
x+3= ![]() (x﹣4)2+
(x﹣4)2+ ![]() ,
,
∴绳子最低点离地面的距离为: ![]() m
m
(2)
解:由(1)可知,BD=8,
令x=0得y=3,
∴A(0,3),C(8,3),
由题意可得:抛物线F1的顶点坐标为:(2,1.8),
设F1的解析式为:y=a(x﹣2)2+1.8,
将(0,3)代入得:4a+1.8=3,
解得:a=0.3,
∴抛物线F1为:y=0.3(x﹣2)2+1.8,
当x=3时,y=0.3×1+1.8=2.1,
∴MN的长度为:2.1m
(3)
解:∵MN=DC=3,
∴根据抛物线的对称性可知抛物线F2的顶点在ND的垂直平分线上,
∴抛物线F2的顶点坐标为:( ![]() m+4,k),
m+4,k),
∴抛物线F2的解析式为:y= ![]() (x﹣
(x﹣ ![]() m﹣4)2+k,
m﹣4)2+k,
把C(8,3)代入得: ![]() (4﹣
(4﹣ ![]() m﹣4)2+k=3,
m﹣4)2+k=3,
解得:k=﹣ ![]() (4﹣
(4﹣ ![]() m)2+3,
m)2+3,
∴k=﹣ ![]() (m﹣8)2+3,
(m﹣8)2+3,
∴k是关于m的二次函数,
又∵由已知m<8,在对称轴的左侧,
∴k随m的增大而增大,
∴当k=2时,﹣ ![]() (m﹣8)2+3=2,
(m﹣8)2+3=2,
解得:m1=4,m2=12(不符合题意,舍去),
当k=2.5时,﹣ ![]() (m﹣8)2+3=2.5,
(m﹣8)2+3=2.5,
解得:m18﹣2 ![]() 4,m2=8+2
4,m2=8+2 ![]() (不符合题意,舍去),
(不符合题意,舍去),
∴m的取值范围是:4≤m≤8﹣2 ![]()
【解析】(1)直接利用配方法求出二次函数最值得出答案;(2)利用顶点式求出抛物线F1的解析式,进而得出x=3时,y的值,进而得出MN的长;(3)根据题意得出抛物线F2的解析式,得出k的值,进而得出m的取值范围.此题主要考查了二次函数的应用以及顶点式求二次函数解析式等知识,正确表示出函数解析式是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y= ![]() x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48. 
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+ ![]() BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+ ![]() BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y= ![]() x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.
x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 分别是
分别是![]() 轴上位于原点两侧的两点,点
轴上位于原点两侧的两点,点![]() 在第一象限,直线
在第一象限,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求![]() ;
;
(2)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(3)若![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,点M,N在同一个正比例函数图象上的是( )
A.M(2,﹣3),N(﹣4,6)
B.M(﹣2,3),N(4,6)
C.M(﹣2,﹣3),N(4,﹣6)
D.M(2,3),N(﹣4,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x+(2m+1)=0有实数根.
(1)求m的取值范围;
(2)如果方程的两个实数根为x1 , x2 , 且2x1x2+x1+x2≥20,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com