
【题目】如图,直线y=﹣2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
【答案】解:∵直线y=﹣2x+4与坐标轴分别交于C、B两点,
∴令y=0,可得﹣2x+4=0,解得x=2,即C(2,0),OC=2,
令x=0,可得y=4,即B(0,4),OB=4,
①如图1,当∠OBC=∠COP时,△OCP∽△BOC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得CP=1,
,解得CP=1,
∴P(2,﹣1),
设过点P的双曲线解析式y=![]() ,把P点代入解得k=﹣2,
,把P点代入解得k=﹣2,
∴过点P的双曲线解析式y=﹣![]() ,
,
②如图2,当∠OBC=∠CPO时,△OCP∽△COB,
在△OCP和△COB中,
∴△OCP≌△COB(AAS)
∴CP=BO=4,
∴P(2,﹣4)
设过点P的双曲线解析式y=![]() ,把P点代入得﹣4=
,把P点代入得﹣4=![]() ,解得k=﹣8,
,解得k=﹣8,
∴过点P的双曲线解析式y=![]() .
.
综上可得,过点P的双曲线的解析式为y=﹣![]() 或y=
或y=![]() .
.
【解析】由直线y=﹣2x+4与坐标轴分别交于C、B两点,易得OC=2,OB=4,再分两种情况①当∠OBC=∠COP时,△OCP与△OBC相似,②当∠OBC=∠CPO时,△OCP与△OBC相似分别求出点的坐标,再求出过点P的双曲线解析式.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
【题目】为迎接河南省第30届青少年科技创新大赛,某中学向七年级学生征集科幻画作品,李老师从七年级12个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图(如图)
(1)李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图补充完整;
(2)李老师所调查的四个班平均每个班征集到作品多少件?请估计全年级共征集到作品多少件?
(3)如果全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,用树状图或列表法求出恰好抽中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为![]()
B.“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件
C.“同位角相等”这一事件是不可能事件
D.“钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点D是![]() 上一点,且∠BDE=∠CBE,BD与AE交于点F.
上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线。
(2)若BD平分∠ABE,求证:DE2=DFDB。
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长和⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
A.18 ![]() ﹣9π
﹣9π
B.18﹣3π
C.9 ![]() ﹣
﹣ ![]()
D.18 ![]() ﹣3π
﹣3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,地面BD上两根等长立柱AB,CD之间悬挂一根近似成抛物线y= ![]() x2﹣
x2﹣ ![]() x+3的绳子.
x+3的绳子. 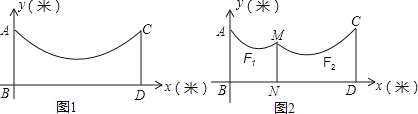
(1)求绳子最低点离地面的距离;
(2)因实际需要,在离AB为3米的位置处用一根立柱MN撑起绳子(如图2),使左边抛物线F1的最低点距MN为1米,离地面1.8米,求MN的长;
(3)将立柱MN的长度提升为3米,通过调整MN的位置,使抛物线F2对应函数的二次项系数始终为 ![]() ,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
,设MN离AB的距离为m,抛物线F2的顶点离地面距离为k,当2≤k≤2.5时,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com