
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足 ![]() .
.
(1)求△ABC的面积;
(2)若tanB=2,求a的值.
【答案】
(1)解:cosA=2 ![]() ﹣1=
﹣1= ![]() ,sinA=
,sinA= ![]() =
= ![]() .
.
∴bc× ![]() =15,可得bc=25.
=15,可得bc=25.
∴S△ABC= ![]() bcsinA=
bcsinA= ![]() =10.
=10.
(2)由tanA= ![]() ,tanB=2,∴tan(A+B)=
,tanB=2,∴tan(A+B)= ![]() =﹣2.
=﹣2.
∴△ABC中,tanC=﹣tan(A+B)=2,
即B=C.∴b=c=5.
∴a2=b2+c2﹣2bccosA=20,解得a=2 ![]() .
.
【解析】(1)cosA=2 ![]() ﹣1,sinA=
﹣1,sinA= ![]() .再利用数量积运算性质可得bc.利用面积计算公式即可得出.(2)tanA=
.再利用数量积运算性质可得bc.利用面积计算公式即可得出.(2)tanA= ![]() ,利用tan(A+B)=
,利用tan(A+B)= ![]() =﹣2.△ABC中,tanC=﹣tan(A+B),及其余弦定理即可得出.
=﹣2.△ABC中,tanC=﹣tan(A+B),及其余弦定理即可得出.
【考点精析】利用余弦定理的定义对题目进行判断即可得到答案,需要熟知余弦定理:![]() ;
;![]() ;
;![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2,ADEF是正方形,在正方形ADEF内部有一点M,满足MB、MC与平面ADEF所成的角相等,则点M的轨迹长度为( )
A.![]()
B.![]()
C.![]()
D.![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市储运部紧急调拨一批物资,调进物资共用4h,调进物资2h后开始调出物资(调进物资与调出物资的速度探持不变).储运部库存物资![]() (t)与时间
(t)与时间![]() (h)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(h)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )

A. 4 h B. 4.4 h C. 4.8 h D. 5 h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地之间的路程为2 380 m,甲、乙两人分别从
两地之间的路程为2 380 m,甲、乙两人分别从![]() 两地出发,相向而行.已知甲先出发5 min后,乙才出发,他们两人在
两地出发,相向而行.已知甲先出发5 min后,乙才出发,他们两人在![]() 之间的
之间的![]() 地相遇,相遇后,甲立即返回
地相遇,相遇后,甲立即返回![]() 地,乙继续向
地,乙继续向![]() 地前行.甲到达
地前行.甲到达![]() 地时停止行走,乙到达
地时停止行走,乙到达![]() 地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程
地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (m)与甲出发的时间
(m)与甲出发的时间![]() (min)之间的关系如图所示,则乙到达
(min)之间的关系如图所示,则乙到达![]() 地时,甲与
地时,甲与![]() 地相距的路程是
地相距的路程是
________m.
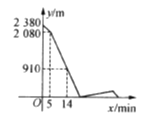
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为  (t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣2ρcosθ﹣4=0
(1)若直线l与曲线C没有公共点,求m的取值范围;
(2)若m=0,求直线l被曲线C截得的弦长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角坐标系中有一矩形OABC , 其中 O是坐标原点,点A , C分别在x轴和y轴上,点B的坐标为(3,4),直线 ![]() 交AB于点D , 点P是直线
交AB于点D , 点P是直线 ![]() 位于第一象限上的一点,连接PA , 以PA为半径作⊙P ,
位于第一象限上的一点,连接PA , 以PA为半径作⊙P , 
(1)连接AC , 当点P落在AC上时, 求PA的长;
(2)当⊙P经过点O时,求证:△PAD是等腰三角形;
(3)设点P的横坐标为m ,
在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图. 
(1)这次被调查的同学共有名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+4与坐标轴分别交于C、B两点,过点C作CD⊥x轴,点P是x轴下方直线CD上的一点,且△OCP与△OBC相似,求过点P的双曲线解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com