
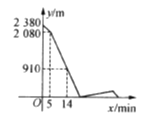
����Ŀ��![]() ����֮���·��Ϊ2 380 m���ס������˷ֱ��
����֮���·��Ϊ2 380 m���ס������˷ֱ��![]() ���س������������.��֪���ȳ���5 min���Ҳų���������������
���س������������.��֪���ȳ���5 min���Ҳų���������������![]() ֮���
֮���![]() ����������������������
����������������������![]() �أ��Ҽ�����
�أ��Ҽ�����![]() ��ǰ��.����
��ǰ��.����![]() ��ʱֹͣ���ߣ��ҵ���
��ʱֹͣ���ߣ��ҵ���![]() ��ʱҲֹͣ���ߣ����������߹����У��ס������˾����ָ��Ե��ٶ��������ߣ��ס�����������·��
��ʱҲֹͣ���ߣ����������߹����У��ס������˾����ָ��Ե��ٶ��������ߣ��ס�����������·��![]() (m)��׳�����ʱ��
(m)��׳�����ʱ��![]() (min)֮��Ĺ�ϵ��ͼ��ʾ�����ҵ���
(min)֮��Ĺ�ϵ��ͼ��ʾ�����ҵ���![]() ��ʱ������
��ʱ������![]() ������·����
������·����
________m.
���𰸡�180
��������
���ݺ���ͼ��ͺ���ͼ���е����ݿ�������ס������˵��ٶȣ���������ҵ���A��ʱ������A��֮���·��.
���ٶ�Ϊ(2380-2080)��5=60����/�֣����ҵ��ٶ�Ϊ(2080-910)��(14-5)-60=70����/�֣���
���Ҵ�B��A�ص�ʱ��Ϊ2380��70=34���֣���
������������ʱ��Ϊ2080��(60+70)=16�����ӣ���
��״ӿ�ʼ��ֹͣ�õ�ʱ��Ϊ(16+5)��2=42�����ӣ���
���ҵ���A��ʱ������A������·����60��(42-34-5)=180���ף�.
�ʴ�Ϊ��180.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=xlnx��mx��ͼ����ֱ��y=��1���У� ������m��ֵ������f��x���ĵ������䣻
������g��x��=ax3 �� ��h��x��=f��x����g��x�������ۺ���h��x������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������2017��3����Ѯ�ٰ���һ��֪ʶ�������������ɸѡ���������ͬѧ�������ܾ������ڽ��бʴ���֪ʶ�����У����һ��������ѡ���⣬Ҫ��μӾ���������ѡ�ִ�2������ѡ��һ�����н�𣬼�����5λѡ��ѡ��ÿһ��Ŀ����Ծ�Ϊ ![]() �� ���������м���2λѡ��ѡ��ͬһ����ĸ��ʣ�
�� ���������м���2λѡ��ѡ��ͬһ����ĸ��ʣ�
��������5λѡ����ѡ����1�������ΪX����X�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=Acos2��x+�գ�+1��A��0����0��0���գ� ![]() �������ֵΪ3��f��x����ͼ����y��Ľ�������Ϊ��0��2���������������Գ����ľ���Ϊ2����f��1��+f��2��+f��3��+��+f��2016����ֵΪ�� ��
�������ֵΪ3��f��x����ͼ����y��Ľ�������Ϊ��0��2���������������Գ����ľ���Ϊ2����f��1��+f��2��+f��3��+��+f��2016����ֵΪ�� ��
A.2468
B.3501
C.4032
D.5739
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڶ�����ABCDEF�У���������BCE����ƽ��������ABCD���ڵ�ƽ�洹ֱ��FD��ƽ��ABCD���� ![]() ��
�� 
��1���ж�ֱ��EFƽ��ABCD��λ�ù�ϵ����˵�����ɣ�
��2������CBA=60�㣬������A��FB��E������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C�ĶԱ߷ֱ�Ϊa��b��c�������� ![]() ��
��
��1�����ABC�������
��2����tanB=2����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ�ȱ������Σ�����B��BD��AC�ڵ�D �� ��D��DE��BC �� ��DE=CD �� ����CE �� 
��1����֤����CDEΪ�ȱ������Σ�
��2��������BE �� ��AB=4����BE�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ����
��ͼ����![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() ���
���![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() �͵�
�͵�![]() ���ҵ�
���ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() .
.
(1)��![]() ��ֵ��
��ֵ��![]() �ij�;
�ij�;
(2)����![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬��
��һ�㣬��![]() �����
�����![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��M��N�ֱ���������ABCD��DC��AB���е㣬�ֱ���AE��BFΪ�ۺۣ�ʹ��D����C����MN�ĵ�G�������ABG�� ������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com