
【题目】已知函数f(x)=Acos2(x+φ)+1(A>0,>0,0<φ< ![]() )的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
)的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
A.2468
B.3501
C.4032
D.5739
【答案】C
【解析】解:∵函数f(x)=Acos2(ωx+φ)+1=A ![]() +1 =
+1 = ![]() cos(2ωx+2φ)+1+
cos(2ωx+2φ)+1+ ![]() (A>0,ω>0,0<φ<
(A>0,ω>0,0<φ< ![]() )的最大值为3,
)的最大值为3,
∴ ![]() +1+
+1+ ![]() =3,可求:A=2.
=3,可求:A=2.
∵函数图象相邻两条对称轴间的距离为2,可得函数的最小正周期为4,即: ![]() =4,
=4,
∴解得:ω= ![]() .
.
又∵f(x)的图象与y轴的交点坐标为(0,2),可得:cos(2φ)+1+1=2,
∴cos2φ=0,2φ= ![]() ,解得:φ=
,解得:φ= ![]() .
.
∴函数的解析式为:f(x)=cos( ![]() x+
x+ ![]() )+2=﹣sin
)+2=﹣sin ![]() x+2,
x+2,
∴f(1)+f(2)+…+f(2016)=﹣(sin ![]() +sin
+sin ![]() +sin
+sin ![]() +…+sin
+…+sin ![]() )+2×2016
)+2×2016
=504×0+4032=4032.
故选:C.
由条件利用二倍角的余弦公式可得f(x)= ![]() cos(2ωx+2φ)+1+
cos(2ωx+2φ)+1+ ![]() ,由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式,再利用函数的周期性求得所求式子的值.
,由函数的最值求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式,再利用函数的周期性求得所求式子的值.


科目:初中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+a.
(1)若不等式f(x)≤6的解集为{x|﹣2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数n使f(n)≤m﹣f(﹣n)成立,求实数m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=axln(x+1)+x+1(x>﹣1,a∈R).
(1)若 ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(2)当x≥0时,不等式f(x)≤ex恒成立,求实数a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设椭圆C1: ![]() +
+ ![]() =1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是
=1(a>b>0),长轴的右端点与抛物线C2:y2=8x的焦点F重合,且椭圆C1的离心率是 ![]() .
. 
(1)求椭圆C1的标准方程;
(2)过F作直线l交抛物线C2于A,B两点,过F且与直线l垂直的直线交椭圆C1于另一点C,求△ABC面积的最小值,以及取到最小值时直线l的方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市储运部紧急调拨一批物资,调进物资共用4h,调进物资2h后开始调出物资(调进物资与调出物资的速度探持不变).储运部库存物资![]() (t)与时间
(t)与时间![]() (h)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )
(h)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( )

A. 4 h B. 4.4 h C. 4.8 h D. 5 h
查看答案和解析>>
科目:初中数学 来源: 题型:
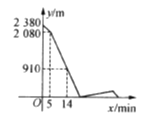
【题目】![]() 两地之间的路程为2 380 m,甲、乙两人分别从
两地之间的路程为2 380 m,甲、乙两人分别从![]() 两地出发,相向而行.已知甲先出发5 min后,乙才出发,他们两人在
两地出发,相向而行.已知甲先出发5 min后,乙才出发,他们两人在![]() 之间的
之间的![]() 地相遇,相遇后,甲立即返回
地相遇,相遇后,甲立即返回![]() 地,乙继续向
地,乙继续向![]() 地前行.甲到达
地前行.甲到达![]() 地时停止行走,乙到达
地时停止行走,乙到达![]() 地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程
地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (m)与甲出发的时间
(m)与甲出发的时间![]() (min)之间的关系如图所示,则乙到达
(min)之间的关系如图所示,则乙到达![]() 地时,甲与
地时,甲与![]() 地相距的路程是
地相距的路程是
________m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角坐标系中有一矩形OABC , 其中 O是坐标原点,点A , C分别在x轴和y轴上,点B的坐标为(3,4),直线 ![]() 交AB于点D , 点P是直线
交AB于点D , 点P是直线 ![]() 位于第一象限上的一点,连接PA , 以PA为半径作⊙P ,
位于第一象限上的一点,连接PA , 以PA为半径作⊙P , 
(1)连接AC , 当点P落在AC上时, 求PA的长;
(2)当⊙P经过点O时,求证:△PAD是等腰三角形;
(3)设点P的横坐标为m ,
在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实数tan45°,![]() ,0,﹣
,0,﹣![]() π,
π,![]() ,﹣
,﹣![]() ,sin60°,0.3131131113…(相邻两个3之间依次多一个1),其中无理数的个数是( )
,sin60°,0.3131131113…(相邻两个3之间依次多一个1),其中无理数的个数是( )
A.4
B.2
C.1
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com