
【题目】已知函数f(x)=|x﹣1|. (Ⅰ)解不等式:f(x)+f(x﹣1)≤2,;
(Ⅱ)若a>0,求证:f(ax)﹣af(x)≤f(a).
【答案】解:(Ⅰ)函数f(x)=|x﹣1|,不等式:f(x)+f(x﹣1)≤2,即|x﹣1|+|x﹣2|≤2, ∴ ![]() ①,或
①,或 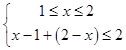 ②,或
②,或 ![]() ③,
③,
解①求得 ![]() ≤x<1,解②求得 1≤x≤2,解③求得2<x≤
≤x<1,解②求得 1≤x≤2,解③求得2<x≤ ![]() .
.
综合可得,不等式的解集为{x| ![]() ≤x≤
≤x≤ ![]() }.
}.
(Ⅱ)证明:若a>0,则f(ax)﹣af(x)=|ax﹣1|﹣a|x﹣1|=|ax﹣1|﹣|ax﹣a|≤|(ax﹣1)﹣(ax﹣a)|=|a﹣1|=f(a),
即f(ax)﹣af(x)≤f(a)成立
【解析】(Ⅰ)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.(Ⅱ)当a>0时,求得f(ax)﹣af(x)=|ax﹣1|﹣|a﹣ax|,利用绝对值不等式的性质可得|ax﹣1|﹣|a﹣ax|≤|ax﹣1+a﹣ax|=f(a),从而可证结论.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:初中数学 来源: 题型:
【题目】哈六中在2017年3月中旬举办了一次知识竞赛,经过层层筛选,最后五名同学进入了总决赛.在进行笔答题知识竞赛中,最后一个大题是选做题,要求参加竞赛的五名选手从2道题中选做一道进行解答,假设这5位选手选做每一题的可能性均为 ![]() . (Ⅰ)求其中甲乙2位选手选做同一道题的概率.
. (Ⅰ)求其中甲乙2位选手选做同一道题的概率.
(Ⅱ)设这5位选手中选做第1题的人数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
月份x | 1 | 2 | 3 | 4 | 5 |
y(万盒) | 4 | 4 | 5 | 6 | 6 |
(1)该同学为了求出y关于x的线性回归方程 ![]() =
= ![]() +
+ ![]() ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出 ![]() =0.6,试求出
=0.6,试求出 ![]() 的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=Acos2(x+φ)+1(A>0,>0,0<φ< ![]() )的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
)的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
A.2468
B.3501
C.4032
D.5739
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接河南省第30届青少年科技创新大赛,某中学向七年级学生征集科幻画作品,李老师从七年级12个班中随机抽取了A、B、C、D四个班,对征集到的作品的数量进行了分析统计,制作了两幅不完整的统计图(如图)
(1)李老师所调查的4个班征集到作品共件,其中B班征集到作品 , 请把图补充完整;
(2)李老师所调查的四个班平均每个班征集到作品多少件?请估计全年级共征集到作品多少件?
(3)如果全年级参展作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生.现在要抽两人去参加学校总结表彰座谈会,用树状图或列表法求出恰好抽中一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com